Karnataka 1st PUC Electronics Question Bank Chapter 2 Principles of Electricity, Network Theorems and AC Principles
One Mark Questions and Answers
Question 1.
What is the unit of electric charge?
Answer:
coulomb (C).
Question 2.
What is the magnitude of the charge of an electron?
Answer:
1.6 × 10-19 C
![]()
Question 3.
Define potential differences.
The potential difference between any two points in a circuit is the amount of work done in moving unit positive charge from one point to another.
Question 4.
Define electric current.
Electric current is defined as the rate of flow of charge through a cross-section of a conductor.
Question 5.
What is the unit of electric current?
ampere (A).
Question 6.
What is the direction of conventional current?
The direction of conventional current is opposite to the direction of the flow of electrons.
Question 7.
Define DC current.
DC current is the current that flows only in one direction and its magnitude remains constant with time.
Question 8.
Define ampere.
The current flowing in a conductor is said to be one ampere if one coulomb of charge flows through the conductor in one second.
Question 9.
Give an example for the DC source.
A battery.
Question 10.
State ohms law.
Ohms law states that current flowing through a conductor is directly proportional to the potential difference across the conductor when the temperature and other physical conditions of the conductor are maintained constant.
Question 11.
Is ohms law applicable when the temperature of a conductor continuously changes?
No.
![]()
Question 12.
Is ohm’s law applicable to semiconductors and insulators?
No.
Question 13.
What is the resistance of a conductor?
Ans. Resistance of a conductor is the opposition offered by it to the flow of current.
Question 14.
Mention the unit of resistance.
Ohm (Q).
Question 15.
What is a node?
Ans.
Node is a point in a circuit where more than two resistors meet.
Question 16.
What is a loop in an electrical circuit?
Answer:
A loop is any closed path in an electrical circuit
Question 17.
When will a load receive maximum power from a source?
Answer:
Load receives maximum power from a source when the load resistance is equal to source resistance.
Question 18.
How is Thevenin’s resistance to a network determined?
Answer:
The venins resistance is the resistance between the open terminals with all sources replaced by their internal resistances.
Question 19.
Write an expression for the instantaneous value of AC Voltage.
Answer:
Instantaneous voltage V = Vm sin ωt.
![]()
Question 20.
How much is the AC voltage applied to all household electrical devices?
Answer:
230V.
Two Mark Questions and Answers
Question 1.
Mention any two properties of charges.
Answer:
- I like charges repel, unlike charges attract.
- Charges always reside on the outer surface of a conductor only.
Question 2.
What is the difference between conventional current and electron current?
Answer:
Conventional current has a direction opposite to that of the flow of electrons. Electron current is in the direction of the flow of electrons.
Question 3.
Mention limitations of Ohms law.
Answer:
- Ohms law is not valid when the physical conditions of the conductor change,
- Ohms law is not valid at very low and very high temperatures.
Question 4.
What are primary sources? Give one example.
Answer:
Primary sources are those which can not be recharged once it is completely discharged, eg., alkaline batteries.
Question 5.
What are secondary DC sources? Give an example.
Answer:
Secondary sources are those which can be recharged, eg lithium-ion batteries used in mobile phones.
![]()
Question 6.
State Kirchhoffs laws.
Answer:
- Kirchhoff’s current law: The sum of currents towards a node is equal to the sum of the currents away from the node.
- Kirchhoff’s voltage law: The algebraic sums of EMFs in any closed loop of a network are equal to the algebraic sum of IR drops in that loop.
Question 7.
What is (i) series combination (ii) parallel combination of resistors?
Answer:
- Series combination is connecting the end of the resistor to the end so that the same current flows; through all of them.
- A parallel combination is connecting the resistors between the same two common points.
Question 8.
Define peak value and RMS value of ac.
Answer:
The peak or maximum value of ac is the maximum voltage or current attained by AC in the half-cycle.
RMS value of ac is the equivalent steady DC value that gives the same heating effect at the same rate in a given resistor.
![]()
Question 9.
Define (i) average value (ii) time period of ac.
Answer:
- Average the mean value of ac is the average of instantaneous voltages of ac taken over the one-half cycle.
- The time period of ac is the time taken to complete one AC cycle.
Question 10.
What is the charge on the body to which 1030 electrons are added?
Answer:
Charge, Q = -ne = -1030 × 1.6 × 10-19 = -1.6 × 1011 C.
Question 11.
How many electrons are to be removed from a body to charge it to 16nC?
Answer:
n = \(\frac{\mathrm{Q}}{\mathrm{e}}=\frac{16 \times 10^{-9}}{1.6 \times 10^{-19}}\) = 10 × 1010 electrons
Question 12.
What are the resistances offered by (i) short circuit (ii) Open circuit?
Answer:
- Zero
- Infinity.
![]()
Question 13.
Draw any two non-sinusoidal AC waveforms.
Answer:
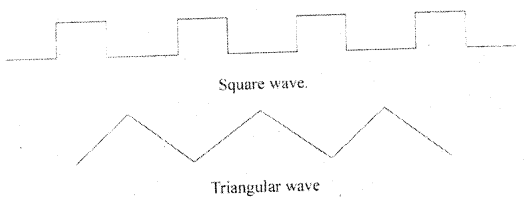
![]()
Three Mark Questions and Answers
Question 1.
Write any three limitations of Ohms law.
Answer:
- Ohm’s law is not valid at very low and very high temperatures.
- When the physical conditions of a conductor change, Ohms law is not valid.
- Ohm’s law is not applicable to semiconductors, discharge tubes, and electrolytes.
Question 2.
State Kirchhoffs laws.
Answer:
- The sum of the currents flowing towards a node in a circuit is equal to the sum of the currents away from the node.
- The algebraic sum of EMFs in any closed loop of a network is equal to the algebraic sum of IR drops in that loop.
Question 3.
What is a voltage source? The row is converted into a current source?
Answer:
The voltage source is that which supplies electrical energy to the circuit in the form of voltage.
RMS value of ac is the equivalent steady DC value which gives the same heating effect at the same rate in a given resistor.
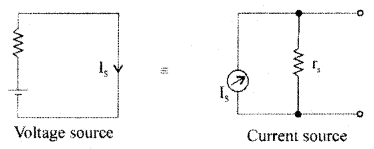
Question 4.
What is a current source? How is it converted into a voltage source?
Answer:
The current source is that which supplies electrical energy to the circuit in the form of current.
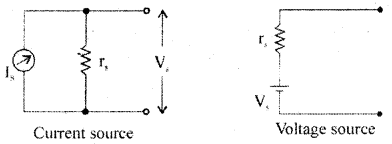
Question 5.
What are linear and nonlinear circuits? Mention one example for each?
Answer:
- Linear Network: In a linear circuit, current and voltage are proportionately varying, an eg. circuit having resistor.
- Non-linear Network: In this circuit, current and voltage are not proportionately varying with each other, eg. circuit having a diode or a transistor.
Question 6.
Mention unit of frequency. Find frequency of an AC whose time period is 10 ms.
Answer:
Frequency of ac is the number of AC cycles completed in one second.
f = \(\frac{1}{T}=\frac{1}{10 \times 10^{-3}}=\frac{1000}{10}\) = 100Hz
Question 7.
What are ideal voltage and current sources? Draw the I-V characteristics of a practical voltage source.
Answer:
The ideal voltage source is the one that supplies a constant voltage to the load irrespective of changes in the load resistance. It has zero resistance. The ideal current source is that which supplies a constant current to the load irrespective of changes in the load. It has infinite resistance.
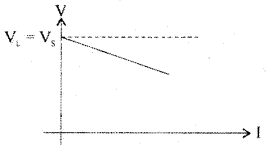
V-I characteristics of Practical voltage Source.
![]()
Question 8.
For the AC waveform given below, find (i) Vrms (ii) Vp (iii) Vavg (IV) frequency.
Answer:
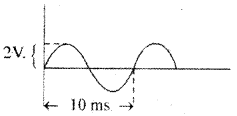
- Vp = 2v
- Vrms = \(\frac{\mathrm{V}_{\mathrm{m}}}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\) = 1.414 volts
- Vavg = \(\frac{2 \mathrm{~V}_{\mathrm{m}}}{\pi}=\frac{2 \times 2}{3.14}\) = 1.27 volt
- f = \(\frac{1}{\mathrm{~T}}=\frac{1}{10 \times 10^{-3}}=\frac{1000}{10}\) = 100Hz
Question 9.
What are non-sinusoidal AC waveforms? Where are they used? Draw square wave and sawtooth wave.
Answer:
Any waveform that is not a sine or cosine wave is called a non-sinusoidal AC waveform.
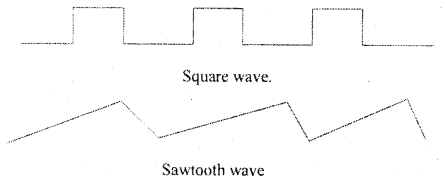
Non-sinusoidal AC waveforms are used in scanning and digital circuit.
Question 10.
What is AC? Why is DC not used for powering all household electrical devices?
Answer:
AC is that whose amplitude varies periodically with respect to time and changes the polarity at regular intervals.
If DC is used for long-distance transmission, the energy losses become too large. Hence, AC is stepped up and transmitted to a large distance with minimum energy losses.
Five Mark Questions and Answers
Question 1.
Mention the properties of charges.
Answer:
- Like charges repel and unlike charges attract each other.
- Charges can neither be created nor be destroyed.
- Charges take only integral values.
- Charges on a body are not affected by the motion of the body.
- Charges always reside only on the outer surface of a conductor only.
![]()
Question 2.
Derive an expression for the effective resistance of resistors connected in series.
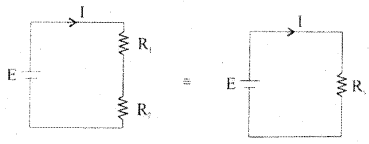
Answer:
Consider two resistors R1 and R2 connected in series to a cell of emf E. In series combination,
the resistors are connected end to end and the same current flows through each of them.
The emf of the cell equals voltage drops across each of the resistors
E = V1 + V2= IR1 + 1R2 {from ohms law}
E = I(R1 + R2) → (1)
The effective or equivalent resistor is a single resistor that has the same effect as a combination of resistors. If Rs. is the effective resistance, E = IR5 – (2)
From the equations (1) and (2), IRs = I(R1 + R2)
∴ Rs = R1 + R2
∴ The effective resistance of resistors in series in the sum of the individual resistances.
Question 3.
Derive an expression for effective resistance of resistors connected in parallel.
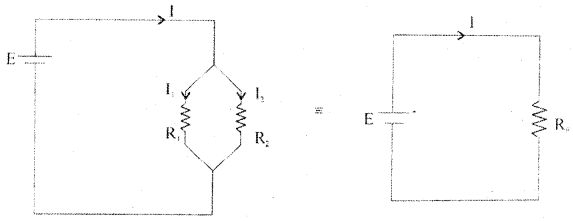
Answer:
Consider two resistors R1 and R2 connected in parallel between the same two common points. In parallel combination, the voltage across each resistor is the same.
Let I1 and I2 be the currents through the resistors R1 and R2.
The current from the cell equals the sum of the currents through the two resistors, i.e.,
I = I1 + I2 = \(\frac{V}{R_{1}}+\frac{V}{R_{2}}\) = V\(\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)\) → (1)
Equivalent or effective resistor Rp is a single resistor that has the same effect as a tile parallel combination. If Rp is the effective resistor, then I = \(\frac{\mathrm{V}}{\mathrm{Rp}}\) → (2)
From equations (1) and (2)
\(\frac{\mathrm{V}}{\mathrm{Rp}}\) = V\(\left(\frac{1}{R_{1}}+\frac{1}{R_{2}}\right)\)
\(\frac{1}{\mathrm{Rp}}=\frac{1}{\mathrm{R}_{1}}+\frac{1}{\mathrm{R}_{2}}\)
Hence, the reciprocal of effective resistance of a number of resistors in parallel is the sum of the reciprocals of the individual resistances.
![]()
Question 4.
Define the following terms (i) Frequency (ii) Time period, (iii) Peak value (iv) RMS value, and (v) peak to the peak value of an ac signal.
Answer:
- The frequency of AC is the number of AC cycles completed in one second.
- The time period of AC is the time taken to complete one cycle.
- The peak value of AC is the maximum voltage or current of the ac in its one of half cycles.
- RMS value of ac is the equivalent steady DC value which gives the same heating effect as the same rate in a given resistor.
- The peak to the peak value of AC is the maximum value attained in both positive and negative half cycles of AC.
Question 5.
State and explain venin’s theorem with an example, or Write a procedure to Venice a given circuit with an example.
Answer:
Venin‘s theorem states that any linear bilateral network having several voltage sources and resistors can be replaced by a simple circuit having one voltage source VTh in series with one single resistor RTh.
Step 1: Identity and remove load resistor RL to convert circuit as a two-terminal network. Mark the two terminals as A and B.
Step 2: To find VTh, calculate the open-circuit voltage between terminals A and B.
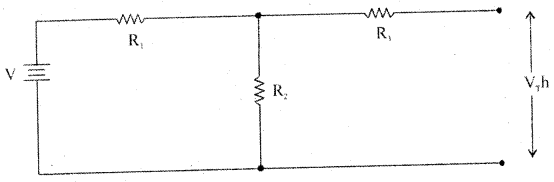
VTh = VR2 = \(\frac{V}{R_{1}+R_{2}}\) × R2
Step 3: To find RTh, replace all voltage sources in the network with their internal resistances and then find the effective resistance between terminals A and B.
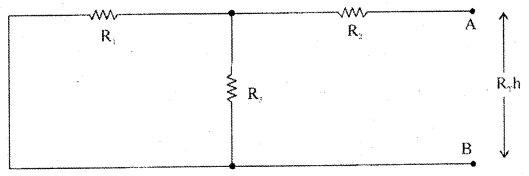
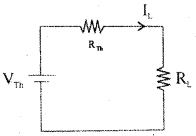
Step 4: Construct Thevenin’s equivalent circuit having VTh in series with RJh and reconnect the load resistor which was earlier removed.
IL = \(\frac{\mathrm{V}_{\mathrm{Th}}}{\mathrm{R}_{\mathrm{Th}}+\mathrm{R}_{\mathrm{L}}}\)
VL = ILRL
![]()
Question 6.
State and explain applying superposition theorem to the given circuit.
Answer:
In any linear bilateral network consisting of two or more independent sources, the resultant current or voltage in any branch is the algebraic sum of the currents or voltages caused by each independent source acting alone, with all other independent sources being replaced by their internal resistances.
Procedure for using Superposition Theorem:
Step 1: Retain the source V, and replace all other sources with their internal resistances.
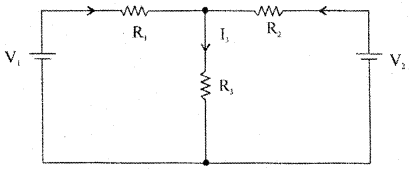
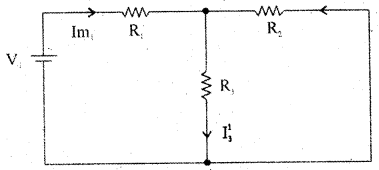
Step 2: Current in various branches and their voltage drops due to V, alone are determined as follows.
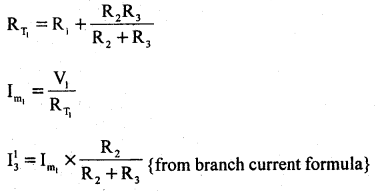
Voltage across R3 = V31 = I31 = I311 = I111 = Im2 × \(\frac{R_{1}}{R_{1}+R_{3}}\)
Step 3: Consider V2 alone and find the currents and voltages as follows :
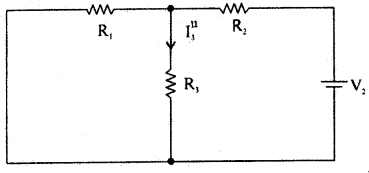
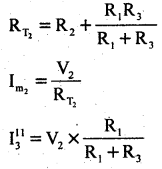
Step 4: Find the algebraic sum of currents and voltage drops in a branch.
I3 = I31 + I311; V3 = I31 R3, V311 = I311 R3
V3 = V31 + V311
![]()
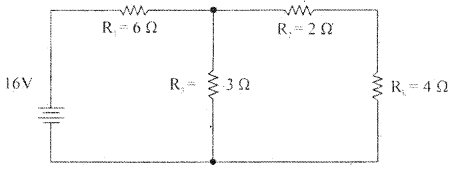
Question 7.
According to the maximum transfer theorem, what should be the value of load resistor RL to get maximum power from the 16V battery as shown in the figure below. What is the value of power across RL?
Answer:
To get maximum power, RL should be equal to Thevenin equivalent resistance.
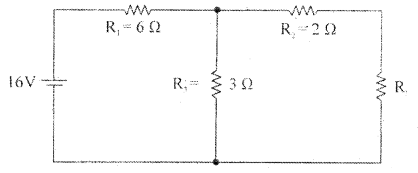
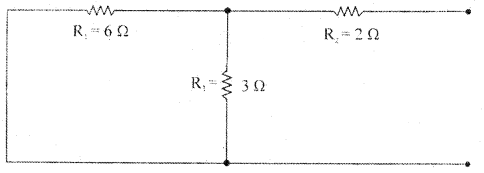
RTh = R2 + \(\frac{\mathrm{R}_{1} \mathrm{R}_{3}}{\mathrm{R}_{1}+\mathrm{R}_{3}}\)
RTh = 2 + \(\frac{6 \times 3}{6 \times 3}\) = 2 + \(\frac{18}{9}\) = 2 + 2 = 4Ω
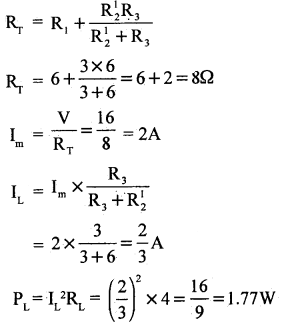
Question 8.
Find the branch currents.
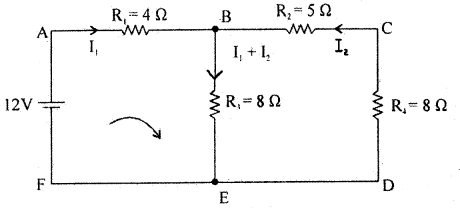
Answer:
Apply KVL to the mesh ABEFA,
I1R1 + 8(I1 + I2) = 12
4I1 + 8 (I1 + I2) = 12
12I1 + 8I2 = 12 (÷4)
3I1 + 2I2 = 3 = → (1)
![]()
Apply KVL to the loop BCDEB,
-R2I2 – R3I2 – R3(I1 + I2) = 0
-5I2 – 3I2 – 8I1 – 8I2 = 0
-8I1 – 16I2 = 0(÷ – 8)
I1 + 2I2 = 0 – (2) .
3I1 + 2I2 = 3 – (1)
-2I1 = -3
I1 + I2 = 1.5 + (-0.75)
I1 = 1.5 A
I1 + I2 = 0.75A
I2 = -0.75 A
Question 9.
Find the load current and load voltage applying Thevenin’s Theorem.
Answer:
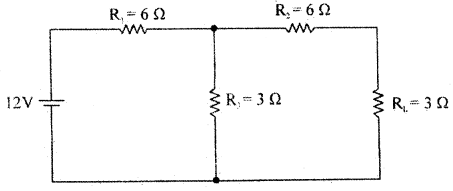
To find RTh
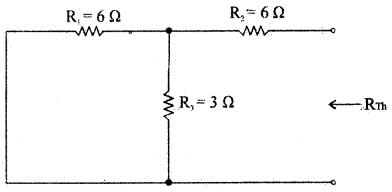
RTh = R2 + \(\frac{\mathbf{R}_{1} \mathbf{R}_{3}}{\mathbf{R}_{1}+\mathrm{R}_{3}}\) = 6 + \(\frac{6 \times 3}{6+3}\) = 6 + 2 = 8
![]()
To find VTh
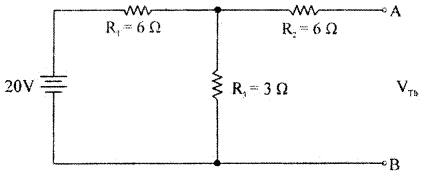
I = \(\frac{V}{R_{1}+R_{3}}=\frac{12}{6+3}\) = 1.33 A
VTh = VAB = IRB= 1.33 × 3 = 3.99 volt.
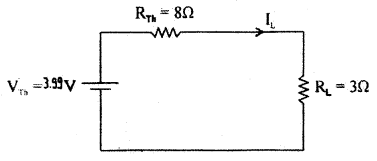
IL = \(\) = 1.09 A
VL = ILRL = 109 × 3 = 3.27 volt
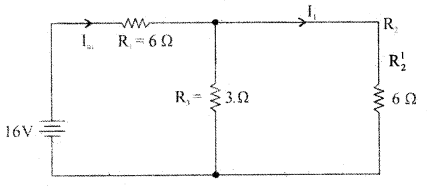
Question 10.
Find the current through 4Ω resistors using superposition theorem.
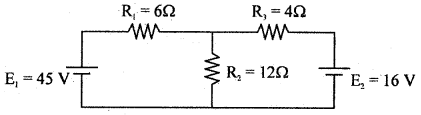
Answer:
Step 1: E1 alone ON and E2 replaced by a short.
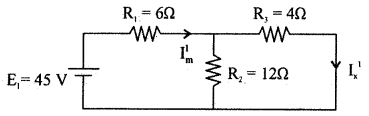
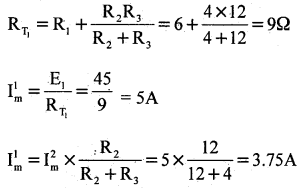
Step 2: E2 alone is ON and E1 replaced by short
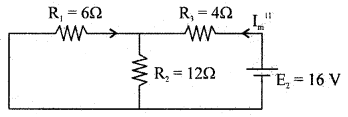
RT2 = R3 + \(\frac{\mathrm{R}_{1} \mathrm{R}_{2}}{\mathrm{R}_{1}+\mathrm{R}_{2}}\) = 4 + \(\frac{6 \times 12}{6+12}\) = 8Ω
Im11 = \(\frac{E_{2}}{R_{T_{2}}}=\frac{16}{8}\) = 2A
From the principle of superposition, current through 4Q resistor is I = Im1 – Im11
= 3.75 – 2 = 1.75A