1st PUC Economics Question Bank Chapter 5 Measures of Central Tendency

Karnataka 1st PUC Economics Question Bank Chapter 5 Measures of Central Tendency

1st PUC Economics Measures of Central Tendency TextBook Questions and Answers

I. Choose the correct Answer

Question 1.
Five students obtained 10, 20, 30, 40, and 50 marks respectively, What would be the mean,
(a) 35
(b) 25
(c) 30
(d) 40
Answer:
(c) 30

Question 2.
…………… = \(\frac{\Sigma X}{N}\) is concerned with
(a) Arithmetic mean
(b) Mode
(c) Median
(d) Geometric mean
(a) Arithmetic mean

Question 3.
The most commonly used measure of central tendency is
(a) Mode
(b) Arithmetic mean
(c) Median
(d) Percentile
Answer:
(b) Arithmetic mean

Question 4.
Which of the following represent median?
(a) Q₁
(b) Q₄
(c) Q₃
(d) Q₂
Answer:
(d) Q₂

Question 5.
Percentiles divide the distribution equally into
(a) 100 parts
(b) 25 pasts
(c) 75 parts
(d) 50 parts
Answer:
(a) 100 parts

Question 6.
Quartiles are the measures that divide the data into
(a) 2 equal parts
(b) 1 equal part
(C) 4 equal parts
(d) 3 equal parts
Answer:
(c) 4 equal parts

Question 7.
The sum of the deviations about mean is
(a) Zero
(b) One
(c) Niinirnum
(d) Maximum
Answer:
(a) Zero

Question 8.
Assigning weights to various items according to their importance is called
(a) Arithmetic mean
(b) Weighted arithmetic mean
(c) Median
(d) Mode
Answer:
(b) Weighted Arithmetic Mean

Question 9.
Median divides the distribution
(a) Into two equal parts
(b) 1st part is more than 2nd part
(c) Into unequal parts
(d) 2nd part is more than 1st part
Answer:
(a) Into two equal parts

Question 10.
The middle value of an ordered series is called
(a) Median
(b) Weighted mean
(c) Mean
(d) Mode
Answer:
(a) Median

Question 11.
Which of the following is the formula for measuring median?

Answer:
(b) Size of \(\frac{(\mathrm{N}+1)^{t h}}{2}\) item

Question 12.
What would be the median wage for the following wages of 5 laborers 10, 20, 30, 35, 38?
(a) Rs. 20
(b) Rs. 25
(c) Rs. 10
(d) Rs. 30
Answer:
(d) Rs. 30

Question 13.
The word ‘mode’ has been derived from
(a) Latin
(b) French
(c) English
(d) German
Answer:
(b) French

Question 14.
The shoe size of most of the people in India is No.7. Which measure of central value does it represent?
(a) Mean
(b) Median
(c) Quartile
(d) Mode
Answer:
(d) Mode

Question 15.
The median is always between
(a) The arithmetic mean and the mode
(b) Quartiles and median
(c) Mode and median
(d) Percentiles and quartiles
Answer:
(a) Tire arithmetic mean and the mode

II. Fill in the blanks

Question 1.
In discrete series……..formula is used to calculate the arithmetic mean.
Answer:
\(\frac{\Sigma X}{N}\)

Question 2.
……arithmetic mean gives relative importance to each item.
Answer:
Weighted

Question 3.
3rd quartile and percentile are the same.
Answer:
75%

Question 4.
There are…………..quartiles in a series.
Answer:
3

Question 5.
A measure that divides the series into hundred equal parts is called
Answer:
Percentiles

Question 6.
Median can be easily located through………..
Answer:
Cumulative frequency

Question 7.
For studying phenomena like intelligence and honesty……….. is a better average
Answer:
Mode

Question 8.
…….is not affected by extreme values.
Answer:
Median

Question 9.
The most frequently observed value in a series is called
Answer:
Mode

Question 10.
A distribution with more than two modes is called
Answer:
Bimodal

III. Match the following

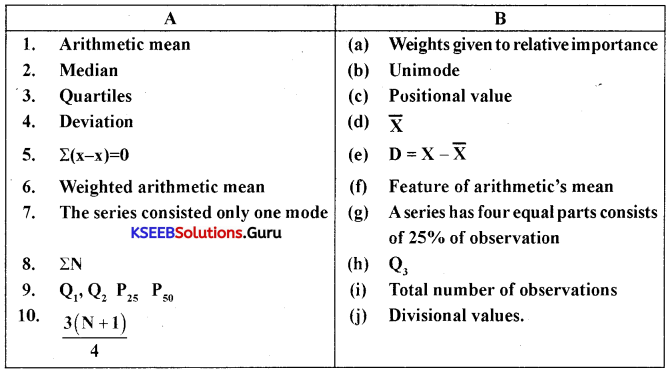
Answer:
1-d. 2-c. 3-g. 4-c. 5-f. 6-a. 7-b. 8-i. 9-j. 10-h.

IV. Answer the following questions in one word or sentence

Question 1.
What is meant by central tendency?
Answer:
Central tendency is one of the statistical tools that summarize the data in a single value in such a way that this single value can represent the entire data.

Question 2.
What is the meaning of arithmetic mean?
Answer:
Arithmetic mean is defined as the sum of the values of all observations divided by the number of observations.

Question 3.
Name any two partition values.
Answer:
Quartiles and percentiles.

Question 4.
Define median.
Answer:
The median is the middle element when the data set is arranged in order of magnitude.

Question 5.
Pocket money of 8 students is Rs. 6,12,18, 24, 30, 36,42 and 48. Calculate the mean. The sum of all the observations is sigma ΣX=215.
Answer:
X̄ = \(\frac{\Sigma X}{N}=\frac{216}{8}\) = 27

Question 6.
Write the relative positions of mean, median, and mode.
Answer:
WM = \(\frac{\Sigma W X}{\Sigma W}\)

Question 7.
Write the relative positions of mean, median, and mode.
Answer:
M_e > M₁ > M_o

Question 8.
Which partition value divides the total set of values into four equal parts?
Answer:
Quartiles.

Question 9.
A shoe manufacturing company manufactures shoes only for adults. As the company wants to know the most popular size, which type of central tendency will be the most appropriate?
Answer:
Mode.

Question 10.
What do you mean by percentiles?
Answer:
Percentiles are those measures that divide the distribution into hundred equal parts.

Question 11.
Give the meaning of quartiles.
Answer:
Quartiles are the measures that divide the data into four equal parts, where each portion contains an equal number of observations.

Question 12.
What type of central tendency is suitable to describe qualitative data?
Answer:
Mode.

Question 13.
What is unimodal?
Answer:
If we get a unique value of mode, then it is called unimodal.

Question 14.
Calculate the mode from the following data:
8,10, 6, 4,12,10, 8,10,18,16, 10,18, 10, 10.
Answer:
10 is the mode as it has the occurred maximum number of tunes.

V. Answer the following Questions in about four sentences

Question 1.
What are the types of measures of central tendency?
Answer:
There are three types of measures of central tendency i.e. mean, median, and mode.

Question 2.
What is a central tendency? Why do we need it?
Answer:
The central tendency is one of the statistical tools which summarizes the data in a single value in such a way that this single value can represent the entire data.

The measure of central tendency is needed to evaluate the relative economic condition. It is a way of summarizing the data in the form of atypical or representative values.

Question 3.
Write the merits of the arithmetic mean.
Answer:
The following are the merits of arithmetic mean:

• It is simple to understand and easy to calculate
• It gives certainty
• It considers all observations in computing
• It is a convenient method of comparison.

Question 4.
Calculate the arithmetic mean from the following data.
(a) Marks obtained by 10 students
30,62,47, 25, 52,39,56, 66,12, 24.
Answer:

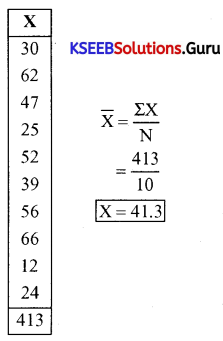
(b) Income of 7 families per week Rs. 550, 490,670,890,435, 590,575
Answer:

Question 5.
Why is the arithmetic mean the most commonly used measure of central tendency?
Answer:
Arithmetic mean is considered as the most commonly used average among all the measures of central tendency. Tins are mainly because it is simple to calculate and it is based tending into account all the observations.

Question 6.
What does weighted arithmetic mean? Give its formula.
Answer:
While calculating the arithmetic means, sometimes, it is essential to give weightage to various items according to their importance. For example, there are two commodities oranges and radish. You are interested in finding the average price of oranges and radish. We may give importance to the rise in the price of oranges for which weights are to be given. To calculate the average of both the products we use weighted arithmetic mean.

Question 7.
Write a note on percentile.
Answer:
Percentiles are the statistical tools used to measure the values by dividing the distribution into hundred equal parts so that we can get 99 dividing positions.

For example, if we have secured 91 percentile in Economics final examination, that means your position is below 9 percent of the total candidates who had appeared in the examination.

Question 8.
What is a quartile? Give the formula to find out Q3.
Answer:
Quantiles are the measures that divide the given data into four equal parts, where each portion contains an equal number of observations.

Question 9.
What is the median? How do you compute it?
Answer:
Median is that positional value of the variable which dí ides the distribution into two equal parts. It is the middle clement when the data set is arranged in order of the magnitudes.
Median can be computed with the help of following formula,
Median = Size of \(\frac{(\mathrm{N}+1)^{t h}}{2}\) item.

Question 10.
Calculate the value of the median (S – 2018)
5,7,9, 12,11,8,7, 15, 25.
Answer:
We need to put in ascending order

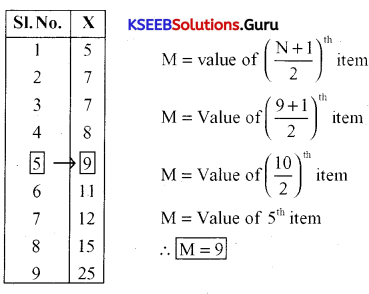
Question 11.
Calculate lower quartile
X: 22, 26, 14, 30, 18, 11, 35, 41, 12, 32
Answer:
First, we need to write in an ascending order

Question 12.
How do you classify modal series?
Answer:
The mode can be classified as follows:
(a) Uni-modal
(b) Bi-modal
(c) Multi-modal.

Question 13.
What is the mode? Give the formula to find out mode in continuous series.
Answer:
The word mode is derived from the French ord la Mode which signifies the most fashionable values of a distribution. because it is repeated the highest number of times in the series. So. mode is the most frequently observed data value,

The following formula is used to calculate mode for a continuous series:
M0 = L + \(\frac{D_{1}}{D_{1}+D_{2}}\) × h

Question 14.
Distinguish between arithmetic mean and weighted mean.
Answer:

Arithmetic Mean	Weighted Mean
Arithmetic mean is defined as the stim of the values of all observations divided by the number of observations	It gives importance to a particular available while calculating the arithmetic mean
It is generally calculated by Σ X/N	It is calculated by \(\frac{q_{1} p_{1}+q_{2} p_{2}}{q_{1}+q_{2}}\)

VI. Answer the following Questions in about twelve sentences.

Question 1.
The daily income often families in a certain locality are given below.

Calculate the arithmetic mean by:
(a) Direct method
(b) Assumed mean method.
Answer:
(a) Direct method

 

(b) Assumed mean method.

Question 2.
Calculate the arithmetic mean from the following data.

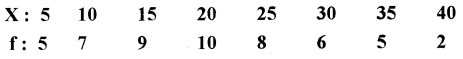
Answer:

Question 3.
Calculate the median from the following data.

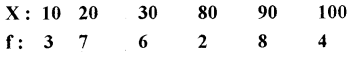
Answer:

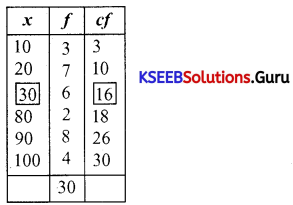
Median = Value of \(\left(\frac{N+1}{2}\right)^{t h}\) item = Value of \(\left(\frac{30+1}{2}\right)^{\text {th }}\) item
= Value of \(\left(\frac{31}{2}\right)^{\text {th }}\) item = 15.5th item is 30
∴ Median = 30

Question 4.
Define weighted mean. How do you calculate it? Explain.
Answer:
While calculating the arithmetic means, sometimes, it is essential to give weightage to various items according to their importance. For example, there are two commodities oranges and radish. You are interested in finding the average price of oranges and radish. We may give importance to the rise in the price of oranges for which weights are to be given. To calculate the average of both the products we use weighted arithmetic mean.

It gives importance to a particular variable while calculating the arithmetic mean. It is calculated with the help of the following formula:
\(\frac{\mathrm{q}_{1} \mathrm{p}_{1}+\mathrm{q}_{2} \mathrm{p}_{2}}{\mathrm{q}_{1}+\mathrm{q}_{2}}\)

Question 5.
Name and define any three statistical averages.
Answer:
There are several statistical measures of central tendency or averages. The most commonly used averages are these:

• Arithmetic mean
• Median
• Mode

(a) Arithmetic mean: It is the most commonly used measure of central tendency. It is defined as the sum of the values of all the observations divided by the number of observations.
It is generally calculated by the formula IX/ N.
The calculation of arithmetic mean can be studied under two broad categories viz.,

• Arithmetic means ungrouped data.
• Arithmetic means for grouped data.

The arithmetic mean can be calculated through the direct method, assumed mean method, and step deviation methods. In each method, a different formula is used.

(b) Median: It is that positional value of the variable which divides the distribution into two equal parts, one part comprises all the values greater than or equal to the median value and the other comprises all values less than or equal to it.

Median is considered as the middle element when the data set is arranged in order of magnitude. It can be easily computed b sorting the data from smallest to largest and counting the middle value,

If there are even numbers in the data. there will be two observations that fall in the middle. The median in this case is computed as the arithmetic mean of the middle values.

In order to calculate the median, it is important to know the position of the median i.e. item at which the median falls. The position of the median can be calculated by the following formula:

Median = Size of \(\frac{(n+1)^{\text {th }}}{2}\) item.

(C) Mode: The word mode is derived from the French word la Mode which means most fashionable values of a distribution. It is the value that is repeated the highest number of times in the series. So mode is the most frequently observed data value. It is indicated by M0.

For continuous series, Mode is calculated with the help of the following formula:
M_o = L + \(\frac{D_{1}}{D_{1}+D_{2}}\) × h

Question 6.
Calculate the Q₁ and Q₃ from the following data.
22, 26, 14, 30. 18, 11, 35, 41, 12, 32.
Answer:

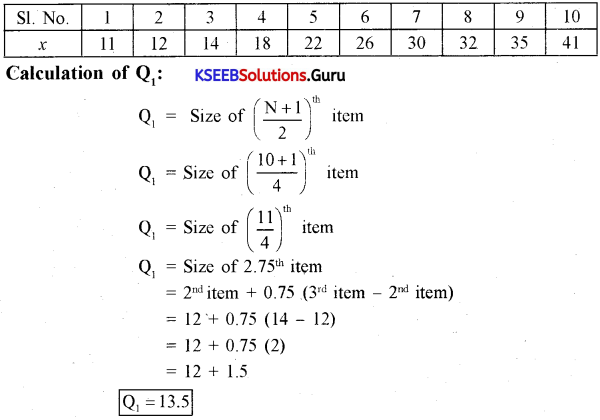
Question 7.
Calculate the median from the following data.

Answer:

Median = Size of Q₃ = 32.75 item
Median = Size of \(\left(\frac{70+1}{2}\right)^{\mathrm{th}}\) item
Median = Size of \(\left(\frac{71}{2}\right)^{\text {th }}\) item

Mediam = 35.5th item i.e. 60
∴ Median = 60

Question 8.
Calculate the mode from the following data.

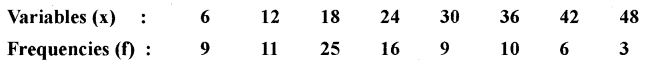
Answer:
Mode =18 (it has occurred highest i.e., 25 times).

Question 9.
Define unimodal, bimodal, and multimodal.
Answer:
The word mode is derived from the French word ‘la Mode’ which means most fashionable values of a distribution. It is the value that is repeated the highest number of times in the series. So Mode is the most frequently observed data value. It is indicated by M_o.

In discrete series, we may come across unimodal, bimodal, and multimodal.
Unimodal: In case there is a unique value of mode, it is called unimodal. Here, there will be only one value that might have occurred the highest times in the series of observations.

For instance: In the series 12, 13, 14, 12, 15, 12, the number 12 has appeared maximum times so it is called unimodal.

Bimodal: In case there are two values that have appeared an equal highest number of times in the given observations, then it is called bimodal.

For instance: In the series 10, 11, 12, 10, 12, 10, 13, 14, 12, the observations 10 and 12 have appeared maximum times, so it is bimodal.

Multimodal: If in given observations, there are more than two observations appeared in the highest numbers then it is called multimodal.

For instance in the series 10, 11, 12. 12, 11, 10, 30, 40, there three values that have occurred more times.

Question 10.
Write a note on quartiles.
Answer:
Quartiles are the measures that divide the data into four equal parts, where each portion contains an equal number of observations. There are three quartiles. They are as follows:

• The first quartile or lower quartile has 25% of the items of the distribution below it and 75% of the items are greater than it.
• The second quartile also called as median, has 50% of the observations above it.
• The third quartile or upper quartile has 75% of the items of the distribution below it and 25% of the items above.

The first or lower quartile is denoted by Q₁, the second quartile or median is denoted by Q₂ and the third quartile or upper quartile is denoted by Q₃.

The first quartile is calculated with the help of following fonnula:
Q₁ = Size of \(\frac{(\mathrm{N}+1)^{\mathrm{th}}}{4}\) item.

The second quartile is calculated with the help of following fonnula:
Median (Q₂) = Size of \(\frac{(N+1)^{t h}}{2}\) item.

The third quartile is calculated with the help of following forumula:
Q₃ = Size of \(\frac{3(\mathrm{~N}+1)^{\mathrm{th}}}{4}\) item.

The method for locating the quartile is the same as that of the median in the case of individual and discrete series.

Question 11.
Write a note on percentiles.
Answer:
Percentiles are tire values that divide the distribution into hundred equal parts. So we can get 99 dividing positions denoted by P₁. P₂, P₃…….. P₉₉, P₅₀ is the median value. If we have secured the 82 percentile in an IAS entrance examination, it means that our position is below 18% of the total candidates who had appeared in the entrance examination.

As stated above, there are 99 percentiles for frequency distribution. These percentiles divide the distribution into hundred equal parts in between two consecutive percentiles, one percent of the value exists.

VII. Answer the following in about twenty sentences

Question 1.
Calculate the arithmetic mean by direct, assumed mean and step deviation methods for the following data.
40, 50, 55, 78, 58.
Answer:

Direct method:
x̄ = \(\frac{\Sigma x}{N}=\frac{281}{5}\)
x̄ = 56.2
Assumed mean method:
x̄ = A + \(\frac{\Sigma d}{\mathrm{~N}}\)
= 40 + \(\frac{81}{5}\)
= 40 + 16.2
x̄ = 56.2
Step deviation method:
x̄ = A + \(\frac{\Sigma d^{\prime}}{\mathrm{N}}\) × c
= 40 + \(\frac{8.1}{5}\) × 10
= 40 + 1.62 × 10
= 40 + 16.2
x̄ = 56.2

Question 2.
Calculate the average marks of the following students using:
(a) Direct method
(b) Step deviation method.

Answer:

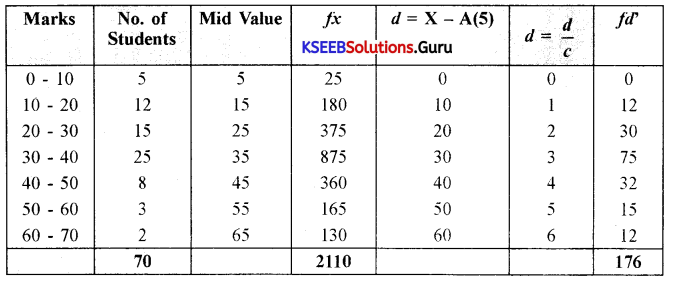
(a) Direct Method:
x̄ = \(\frac{\Sigma f x}{N}=\frac{2110}{70}\) = 30.14

(b) Step Deviation Method:
x̄ = A + \(\frac{\Sigma d^{\prime}}{\mathrm{N}}\) × c
= 5 + \(\frac{176}{70}\) × 10
= 5 + 2.514 × 10
= 5 + 25.14
x̄ = 30.14

Question 3.
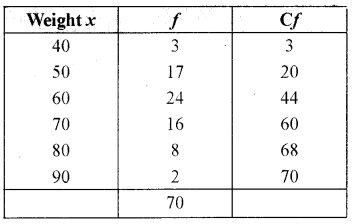
The following data relates to the daily wages of persons working in a factory. Compute the median daily wages.

Answer:


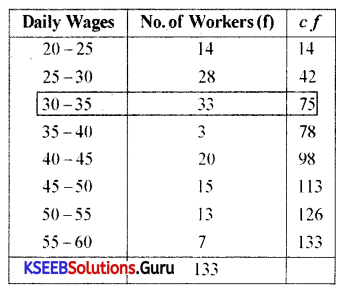
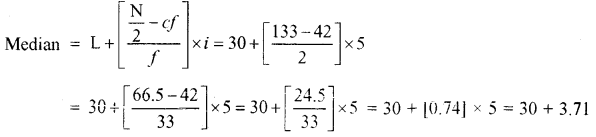
M = 33.71
where L – Lower limit
CF – cumulative frequency of preceding median
F – Frequency of median
I – Magnitude of median class.

Question 4.
Find the median of the following data.

Answer:

Question 5.
Calculate the Q₁ Q₂, and Q₃ front the following data
15, 21, 26, 30, 40, 45, 50, 54, 60, 65, 70.
Answer:

Question 6.
Calculate the Q₁ Q₂ and Q₃ from the following data.
22, 26, 14, 30, 18, 11, 35, 41, 12, 32. (Board Paper)
Answer:

i.e., 2nd item + 0.75 (3rd item – 2’ item)
Q = 12 + 0.75 (14 – 12) = 12 + 0.75 (2) = 12 + 1.5
Q₁ = 13.51

Calculate of Q₂:

Question 7.
Calculate the value of a worker family’s is daily modal income from the following data.

Answer:

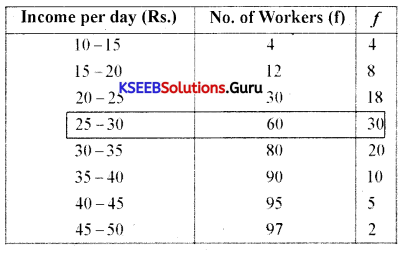
From the above table, we can locate 25 – 30 as a modal group as it has occurred maximum times.
To find exact mode, the following formula is used:

L = Lower limit of modal class.
D₁ = Difference between frequency of the model class and frequency of preceding modal class.
D₂ = Difference between frequency of the modal class and frequency of succeeding modal class.
h = Class interval of the distribution.

Question 8.
Calculate the mode from the following distribution. (S – 2018)

Answer:

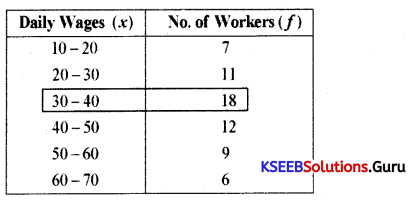
By seeing the frequency column, we can make out that the class interval 30-40 is considered as the modal group. To find out the exact mode the following formula is used.

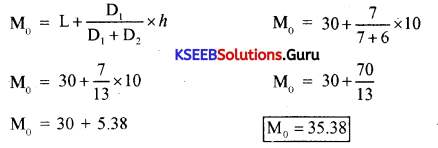
VIII. Project-oriented Question

Question 1.
As per the recorded temperature, every two hours in a day from 6 am to 6 pm calculate the range and mean temperature of the day.

Hours	Temperature
6 – 8 am	25° celsius
8 – 10 am	26° celsius
10 – 12 am	28° celsius
12 – 2 pm	34° celsius
2 – 4 pm	35° celsius
4 – 6 pm	30° celsius
	178

Ranges = Laigest – Smallest = 35 – 25
Range = 10° ceLsius

Mean temperature of the day
x̄ = \(\frac{\Sigma x}{\mathrm{~N}}=\frac{178}{6}\)
x̄ = 29.66
N = Number of observation
Σx = Sum of temperatures during the day
The mean temperature of the day is 29.66° Celsius.

1st PUC Economics Measures of Central Tendency Additional Questions and Answers

Question 1.
Which average would be suitable in the following cases?
(a) Average size of readymade garments.
Answer:
Mode

(b) Average performance of students in a class
Answer:
Median

(c) Average production in a factory per shift.
Answer:
Arithmetic mean

(d) Average wage in an industrial concern.
Answer:
Arithmetic mean

(e) When the sum of absolute deviations from average is the least.
Answer:
Arithmetic mean

(f) When quantities of the variable are in ratios.
Answer:
Median

(g) In the case of open-ended frequency distribution.
Answer:
Median

Question 2.
Indicate the most appropriate alternative from the multiple choices provided against each question.
(i) The most suitable average for qualitative measurement is
(a) Arithmetic mean
(b) Median
(c) Mode
(d) Geometric mean
(e) None of these
Answer:
(b) Median

(ii) Which average is affected the most by the presence of extreme items?
(a) Median
(b) Mode
(c) Arithmetic mean
(d) Geometric mean
(e) Harmonic mean
Answer:
(c) Arithmetic mean

(iii) The algebraic sum of deviation of a set of n values from the arithmetic mean is
(a) n
(b) 0
(c) 1
(d) None of these
Answer:
(b) 0 .

Question 3.
Comment whether the following statements are true or false.
(i) The sum of deviation of items from the median is zero.
Answer:
False. The sum of deviations of items from the median will be minimum and not be zero.

(ii) An average alone is not enough to compare series.
Answer:
True. Apart from averages, there are other measurements to compare series.

(iii) Arithmetic mean is a positional value.
Answer:
False. Itisamathematicalaveragewhichtakesall values in a given observation. Median is positional value.

(iv) Upper quartile is the lowest value of the top 25% of items.
Answer:
True. The upper quartile divides the distribution as 75% of total items fall less than 75 and 25% above 75%.

(v) Median is unduly affected by extreme observations.
Answer:
False. Median is a positional value. It is not influenced by any extreme values.

Multiple Choice Questions with Answers

Question 1.
Mean of 7, 3, 6, 9,0, 5,12,0, 5 is
(a) 3.6
(b) 5.2
(c) 5.6
(d) 4.9
Answer:
(b) 5.2

Question 2.
The summation of deviations about the arithmetic mean will be
(a) 0
(b) 1
(c) Highest
(d) Lowest
Answer:
(a) 0

Question 3.
The measures of central tendency are also called as:
(a) Differentiation
(b) rages
(c) Integration
(d) Integration
Answer:
(b) Acres

Question 4.
The most widely used average is
(a) Medium
(b) Mode
(c) Arithmetic mean
(d) None of these
Answer:
(c) Arithmetic mean

Question 5.
The most frequently occurring value in a series is called
(a) Quartiles
(b) Median
(c) Geometric mean
(d) Mode
Answer:
(d) Mode

Question 6.
The mode of 4, 6, 8,5,9, 7,5 is
(a) 4
(b) 5
(c) 9
(d) 7
Answer:
(b) 5

Question 7.
Median of 9, 5,8, 4,10,6, 7, 2 is
(a) 6
(b) 10
(c) 2
(d) 8
Answer:
(a) 6

Question 8.
CF is a short form used for
(a) Common value
(b) Cumulative frequency
(C) Common factor
(d) None of the above
Answer:
(b) Cumulative frequency

Question 9.
A frequency distribution having two modes is said to be
(a) Unimodal
(b) Bimodal
(c) Trimodal
(d) None of these
Answer:
(b) Bimodal

Question 10.
The histogram is useful to determine graphically the value of
(a) Mean
(b) Median
(c) Mode
(d) All the above
Answer:
(c) Mode

Very Short Answers Type Questions with Answers

Question 1.
What do you mean by the arithmetic mean?
Answer:
It is the sum of all items divided by the number of observations.

Question 2.
What would be the sum of deviations of individual items taken from the arithmetic mean?
Answer:
Zero.

Question 3.
Name the appropriate method for the common factor of the deviation of the items.
Answer:
Step deviation method.

Question 4.
What would you get if the sum of items is divided by their number?
Answer:
Mean.

Question 5.
How do you measure arithmetic mean for open-end series?
Answer:
In open-end series, we have to assume that the unknown classes which depend on the pattern of class intervals of other classes.

Question 6.
What is the median?
Answer:
Median is the middle value in the data set when its elements are arranged in sequential order.

Question 7.
What do you call the measure which divides the series into four equal parts?
Answer:
Quartiles.

Question 8.
Show the relationship between mean, mode, and median.
Answer:
Mode = 3 median – 2 mean.

Question 9.
Name the graph used to locate median graphically
Answer:
Ogive curve.

Question 10.
Name the graph used to compute mode.
Answer:
Histogram.

1st PUC Economics Question Bank with Answers