Karnataka 1st PUC Economics Question Bank Chapter 3 Organisation of Data
1st PUC Economics Organisation of Data TextBook Questions and Answers
I. Choose the correct answer
Question 1.
The class midpoint is equal to
(a) The average of the upper-class limit and the lower class limit.
(b) The product of the upper-class limit and the lower class limit.
(c) The ratio of the upper-class limit and the lower class limit.
(d) None of the above.
Answer:
(a) The average of the upper-class limit and the lower class limit.
![]()
Question 2.
The frequency distribution of two variables is known as
(a) Univariate distribution
(b) Bivariate distribution
(c) Multivariate distribution
(d) None of the above
Answer:
(b) Bivariate distribution
Question 3.
Statistical calculations in classified data are based on
(a) The actual values of observations
(b) The upper-class limits
(c) The lower class limits
(d) The class midpoints
Answer:
(d) The class midpoints
Question 4.
Under the exclusive method,
(a) The upper-class limit of a class is excluded in the class interval.
(b) The upper-class limit of a class is included in the class interval.
(c) The lower class limit of a class is excluded in the class interval.
(d) The lower class limit of a class is included in the class interval.
Answer:
(a) The upper-class limit of a class is excluded in the class interval.
Question 5.
Range is the
(a) Difference between the largest and title smallest observations.
(b) Difference between the smallest and the largest observations.
(c) Average of the largest and the smallest observations.
(d) Ratio of the largest to the smallest observation.
Answer:
(a) Difference between the largest and the smallest observations.
II. Fill in the blanks
Question 1.
Data classified according to geographical areas is called………………
Answer:
Spatial classification
![]()
Question 2.
Classification of data according to characteristics and attributes is called…………………….
Answer:
Qualitative classification
Question 3.
The two ends of a class are called…………
Answer:
Class limits
Question 4.
………………….is the average of upper and lower limits of a class.
Answer:
Class limits
Question 5.
In ……… method of classification upper limit of a class is included.
Answer:
Inclusive
Question 6.
Frequency distribution of discrete frequency is called ………………
Answer:
Frequency array
Question 7.
……………is the frequency distribution of a single variable.
Answer:
Univariate distribution
![]()
III. Answer the following questions in a word/sentence.
Question 1.
What is raw data?
Answer:
The data which is not classified is called raw 7 data.
Question 2.
What do you mean by qualitative classification of data?
Answer:
When the data is classified on the basis of certain attributes or characteristics like, gender, literacy, employment, etc., it is called qualitative classification.
Question 3.
What is a quantitative classification of data?
Answer:
When the data is classified on the basis of certain characteristics like height, age, income, etc., it is called as quantitative classification of data.
Question 4.
Give the meaning of class limits.
Answer:
The two ends of a class interval are called class limits.
Question 5.
Write the meaning of midpoint in a class.
Answer:
The midpoInt in a class refers to the middle value of the class limits.
Question 6.
What is a univariate frequency distribution?
Answer:
The univariate frequency is a frequency distribution of a single variable.
![]()
Question 7.
What is a bivariate frequency distribution?
Answer:
The bivariate frequency is a frequency distribution of two variables.
Question 8.
Write the meaning of the frequency array.
Answer:
Frequency array refers to the classification of a discrete variable.
Question 9.
Give the meaning of time series data.
Answer:
When the data is classified according to time. it is called time-series data.
Question 10.
What is a spatial classification of data?
Answer:
When the data is classified with reference to geographical location, it is called spatial classification
IV. Answer the following questions in about four sentences
Question 1.
Mention the types of variables. . (N-2018)
Answer:
There are two types of variables namely. Continuous variable and discrete variable.
![]()
Question 2.
Differentiate between inclusive and exclusive methods of classification. (Board Paper)
Answer:
Exclusive method: Under this method, the class is formed in such a way that the upper-class limit of one class will be equal to the lower class limit of the next class. Here, the continuity of the data is maintained. This method is most suitable in the case of data of a continuous variable.
For example. among class intervals l0-2() and 20-30. 20 is included in the next class interval i.e. 20-30and not in 10-20.
Inclusive method: Under this method. upper-class limit is included in a class interval, So here. both upper-class limit and lower class limit are Parts of the class interval.
In the above example. if we take the class interval 10-19. the lower limit. 10 and the upper 19 are included in the class interval 10-19. If e consider the class intervals as marks of students. the marks scored b students between 10 and 19 falls in this class internal. If a student secures 20. it falls in the next class interval,
Question 3.
Mention the types of classification of data.
Answer:
The hopes of classification of data are
(a) Quantitative classification.
(b) Qualitative classification
(C) Chronological classification.
(d) Spatial classification.
Question 4.
Give the formula to find out the midpoint (S – 2018)
Answer:
The formula to find out midpoint is as follows:
Mid point = \(\frac{\text { Upper class limit }+\text { Lower class limit }}{2}\)
![]()
Question 5.
What is the frequency?
Answer:
Frequency refers to how many times the observations have occurred in the given raw data. In other words. frequency refers to the number of times a given aItie appears in a distribution.
V. Answer the following questions in about twelve sentences
Question 1.
Briefly explain ‘Loss of the information in classified data.
Answer:
In a classification of data. summarizing the raw data. making it concise and comprehensible. does not show the details that are found in raw data. There is a loss of information in classifying raw data though much is gained b summarizing it as classified data. Once the data are grouped into classes, an individual observation has no significance in further statistical calculations. This is known as the loss of information in classified data.
For example. suppose class I00-200contains6 values viz,, 120, 150, 160. 140. 180. 190. When such data is grouped as a class 100-200. then individual values have no significance and only frequency i.e. 6 is recorded and not their actual aliens. All values in this class are assumed to be equal to the middle value of the class-interval or class mark. Statistical calculations are based only on the values of class marks instead of the actual values. As a result, it leads to considerable loss of information.
Question 2.
Differentiate between continuous and discrete variables are as follows.
Answer:
| Continuous Variable | Discrete Variable |
| It can take any numerical value. | It can take only certain values. |
| It may take integral values, fractional values, and values that are not exact fractions. | Its value changes only by finite ‘jumps’. It ‘jumps’ from one value to another, but does not take any intermediate value. |
| For example, the height of a student, as he grows say from 100 to 150 cm. would take all the values in between 100 and 150. | For example, a variable like the ‘number of girls in a class’, for different classes, would assume values that are only whole numbers. It cannot take any fractional value like 0.5 because ‘half of a student’ is absurd. |
| The variable is capable of manifesting in every conceivable value and its values can also be broken down into infinite gradations. | It takes a value change from 100 to 101. 102 etc, but fractions are not taken it i.e., there cannot be 100.1, 100.5, etc. |
| Other examples of a continuous variable are weight, time, distance, etc. | Other examples for a discrete variable are population, number of cars, buses, and number appearing on a dice. |
![]()
Question 3.
Write a note on the classification of data. (S – 2018) (N – 2018) (Board Paper)
Answer:
The raw data are classified in various ways depending on the purpose. Generally, data can be classified as follows:
(a) Chronological classification: When the data is grouped according to time, it is called chronological classification. In such a classification, data are classified either in ascending or in descending order with reference to time such as years, quarters, months weeks days, etc.
(b) Spatial classification: If the data are classified with reference to geographical locations such as countries, states, cities, districts, etc., it is called spatial classification.
(c) Qualitative classification: When the data are classified on the basis of certain attributes
or qualities like literacy, religion, gender, marital status, etc., then it is called qualitative classification. These attributes can be classified on the basis of either the presence or the absence of a qualitative characteristic.
(d) Quantitative classification: If the classification of data is done on the basis of certain characteristics like height, weight, age, income, marks of students, etc., it is called quantitative classification.
VI. Answer the following in about twenty sentences
Question 1.
Prepare a frequency distribution by inclusive method taking class interval of 7 from the following data.

Answer:
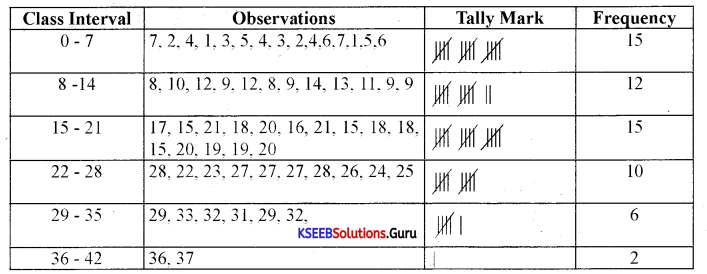
Question 2.
Explain frequency distribution with unequal classes with an example.
Answer:
Sometimes we may think that in some cases frequency distributions with unequal class intervals are more appropriate. Lets us consider the following example:

In the above table, we notice that most of the observations are concentrated in classes 40-50. 50-60 and 60-70. Their frequencies are 21. 23 and 19. It means that out of 85 students. 63 students are concentrated in these classes. Thus, about 74 percent of students are in the middle of the 40-70 range.
![]()
Further, we can also notice that the observations in these classes deviate more from their respective class marks than in comparison to those in other classes. But if classes are to be formed in such a way that class marks coincide, as far as possible, to a value around which the observations in a class tend to concentrate, then the unequal class interval is more appropriate.
Question 3.
List the four questions to be addressed while preparing a frequency distribution. Explain any two of them.
Answer:
While preparing frequency distribution, the following four questions need to be addressed:
(a) How many classes should we have?
(b) What should be the size of each class?
(c) How should we determine the class limits?
(d) How should we get the frequency for each class?
(a) How many classes should we have?
Before solving this question, we need to first find out to what extent the variable in hand changes in value. Such variations in the value of variables are captured by their range. The range is the difference between the largest and smallest values of a variable. A large range indicates that the values of the variable are widely spread. On the other hand, a small range indicates that the values of the variable are spread narrowly.
After obtaining the value of the range, it becomes easy to determine the number of classes once we decide the class interval.
![]()
Given the value of the range, the number of classes would be large if we choose small class intervals. A frequency distribution with too many classes would look too large. Such a distribution is not easy to handle. So we want to have a reasonably compact set of data. On the other hand, given the value of range if we choose a class interval that is too large then the number of classes becomes too small. The data set then maybe too compact and we may not like the loss of information about its diversity.
For example, suppose the range is 100 and the class interval is 50, then the number of classes would be just 2. Though there is no hard and fast rule to determine the number of classes, the rule of thumb often used is that the number of classes should be between 5 and 15.
(b) What should be the size of each class?
It is well said that, given the range of the variable, we can determine the number of classes once we decide the class interval. Similarly, we can determine the class interval once we decide the number of classes. Thus, we find that these two decisions are interlinked with one another. We cannot decide on one without deciding on the other.
1st PUC Economics Organisation of Data Additional Questions and Answers
Question 1.
Can there be any advantage in classifying things? Explain with an example from your daily life.
Answer:
Classification is organizing things into groups or classes based on some criteria. There will be advantages in classifying things as classification of objects or things saves our valuable time and effort.
For example, we can classify books according to subjects, date of purchase, authors, etc. If we classify history books under the group history, we would not put a book of a different subject in that group. Otherwise, the entire purpose of grouping would be lost.
If we go to a medical shop, we can see varieties of medicines kept for sale. The medicines are ‘ classified on the basis of diseases so that they are easily available to give immediately to the patients.
From the above explanation, it is clear that the classification of things is definitely helpful in our daily life.
Question 2.
In a city, 45 families were surveyed for the number of cell phones they owned. Prepare a frequency array based on their replies as recorded below:

Answer:

Question 3.
Do you agree that classified data is better than raw data? Why?
Answer:
Yes, classified data is better than raw data. This is because classification brings order to raw data. Further, raw data are summarized and made comprehensible by classification. It enables one to locate them easily, make comparisons and draw inferences without any difficulty. Hence, classified data is better than raw data.
Question 4.
Distinguish between univariate and bivariate frequency distributions.
Answer:
The frequency distribution of a single variable is called a univariate distribution. For example, the distribution of marks of a student.
![]()
Whereas, a bivariate frequency distribution refers to the frequency distribution of two variables. For example, the frequency distribution of two variables – sales and advertisement cost of 10 companies.