Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2017 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2017 (South)
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any TEN questions. (10 × 1 = 10)
Question 1.
Write the imaginary part of 3 – Imaginary part of 3 – i is -1.
Answer:
The imaginary part of 3 – i is -1
Question 2.
If A has 4 elements, how many elements, how many elements will P(A) have.
Answer:
P(A) will have 16 Elements.
Question 3.
If R-1 = {(2, 4) (1, 2) (3, 1) (3, 2)} find R.
Answer:
R= {(4, 2) (2,1) (1,3) (2, 3)}.
Question 4.
Simplify: (22)2 – 2(3°)
Answer:
= 1 – 2′ = 1 – 2 = -1
![]()
Question 5.
Solve for x if log7 x = 2.
Answer:
x = 72 = 49.
Question 6.
Find the sum to infinity of the GP 3,1, \(\frac{1}{3}\), ……………
Answer:
Sn = \(\frac{a}{1-r}=\frac{3}{1-\frac{1}{3}}=\frac{9}{3-1}=\frac{9}{2}\)
Question 7.
Form the quadratic equation whose roots are 2, 3.
Answer:
(x – 2)(x – 3) = 0 ⇒ x2 – 5x + 6 = 0.
Question 8.
What is the simple interest on 650 for 14 weeks at 6% p.a?
Answer:
S.I = 650 × \(\frac{14}{52} \times \frac{6}{100}\) = 10.5
![]()
Question 9.
The average score of 35 girls is 80 and the average score of 25 boys ¡s 68. Find the average score of both boys and girls together.
Answer:
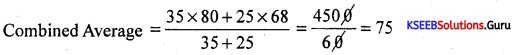
Question 10.
By selling a book at’ 250 the profit made is ₹ 50. What is the cost price of the book?
Answer:
C.P = S.P – Profit = 250 – 50 = 200₹.
Question 11.
Convent 315° to radians.
Answer:
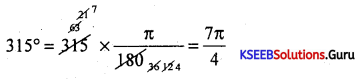
Question 12.
Find the slope of the line 2x + 5y – 11 = 0.
Answer:
Slope = –\(\frac{2}{5}\)
Part – B
II. Answer any TEN questions. (10 × 2 = 20)
Question 13.
Find the number of positive divisors of 360.
Answer:
360 = 23 × 32 × 51
n = P1α1. P2α2. P3α3
T(n) = T(360) = (1 + α1) (1 + α2) (1 + α3) = (3 + 1) (2 + 1) (1 + 1) = 24.
∴ If has 24 positive divisors.
![]()
Question 14.
Find the HCF of two numbers if their LCM is 1260 and product is 52920.
Answer:
H.C.F = \(\frac{a \times b}{\mathrm{LCM}}=\frac{52920}{1260}=\frac{5292}{126}\) = 42
Question 15.
If f(x) = x, g(x) = x3 + 1 find (a) fog (2) (b) gof (1)
Answer:
fog (2) = f(g (2)) = f( 23 + 1) = f( 9) = 9
gof(1) – g (f(1)) = g (1) = 13 + 1 = 1 + 1 = 2.
Question 16.
Find the domain and range of the relation R = {(x, y): y = x2, x is a positive prime number less than 10}
Answer:
R= {(2,4)'(3, 9) (5,25) (7, 49)}
Domain – {2, 31 5, 7}, Range = {4,9,25, 40}.
Question 17.
If a = 3x b = 3y c = 3z and ab – c2. P.T. x + y = 2z.
Answer:
Given ab = c2
3x.3y = (32z) ⇒ 3x+y = 32z
x + y = 2z.
![]()
Question 18.
Insert 3 Arithmetic means between -2 and -10.
Answer:
Let A1, A2, A3 are 3 A.m between -2 and -10
∴ -2, A1, A2, A3………. -10 are in A.P .
a a + d a + 2d a + 3d a + Ad are in A.P
∴ a = – 2 and a + 4d = – 10 ⇒ 4d = -10 + 2 = -8
d = – 2 .
Hence A1 = -2 – 2 = -4,
A2 = a + 2d = – 2 – 4 = – 6,
A3 = a + 3d = -2 – 6 = -8
Hence 3 Ams are -4, -6, and -8.
Question 19.
If a and b are the roots of the equation 2x2 + 5x + 5 = 0 the find the value of \(\frac{1}{\alpha}+\frac{1}{\beta}\)
Answer:
Given 2x2 + 5x + 5 = 0
α + β = \(\frac{-b}{a}=\frac{-5}{2}\)
αβ = \(\frac{c}{a}=\frac{5}{2}\)
\(\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\alpha+\beta}{\alpha \beta}=\frac{-5 / 2}{5 / 2}\) = -1
Question 20.
Solve 7x + 3 < 5x + 9, x∈R and represent on number line.
Answer:
7x + 3 < 5x + 9

7x – 5x <9 – 3
2x < 6
x < 3
∴ Solution set is (- ∞, 3)
Question 21.
Find the effective rate of interest when a sum lent at 12% is computed half yearly.
Answer:
r = \(\left(1+\frac{i}{q}\right)^{q}\) – 1 = \(\left(1+\frac{0.12}{2}\right)^{2}\) – 1
= (1 + 0.06)2 – 1 =(1.06)2 – 1 = 12.36.
Question 22.
The average age of 12 boys is 8 years. Another boy of 21 years joins the group. Find the average age of the new group.
Answer:
Ave age of 12 boys = 8 yrs.
∴ Total age of boys = 8 x 12 = 96 yrs.
When a boy of 21 yrs joins the group
∴ Total age of the 13 boys = 96 + 21 = 117 yrs.
∴ Average age of the new group = \(\frac{117}{13}\) = 9 yrs.
Question 23.
Find the value of sin (480°) + tan 135°.
Answer:
sin (480°) + tan (135°) = sin (360 + 120) + tan (180 – 45)
= sin 120-tan 45
= sin (180 – 60) – 1 = sin 60 – 1 = \(\frac{\sqrt{3}}{2}\) – 1
![]()
Question 24.
The CEO the triangle ABC is the point (2, 3). The coordinates of A are (5, 6) and B(-l, 4). Find the coordinates of C.
Answer:
G(x, y) = \(\left(\frac{x_{1}+x_{2}+x_{3}}{3}, \frac{y_{1}+y_{2}+y_{3}}{3}\right)\), C(x3, y3) = ?
(2, 3) = \(\left(\frac{5-1+x_{3}}{3}, \frac{6+4+y_{3}}{3}\right)\)
(2, 3) = \(\left(\frac{4+x_{3}}{3}, \frac{10+y_{3}}{3}\right)\) ⇒ 6 = 4 + x3,
10 = y3 = 9
⇒ x3 – 6 – 4, y3 = 9 – 10
⇒ x3 = 2, y3 = -1
Hence co-ordinates of C(x3, y3) = C(2, – 1)
Question 25.
Find equation of line passing through (0, -4) and making an angle of 30° with the x-axis.
Answer:
Required equation is y – y1 = m(x – x1)
i.e., (y – (-4) = tan 30° (x = 0)
y + 4 = \(\)(x)
x = \(\sqrt{3}\)y + 4\(\sqrt{3}\) = 0
Part-C
III. Answer any TEN questions. (10 × 3 = 30)
Question 26.
Find the number which when divided by 36, 40 and 48 leaves the same remainder 5.
Answer:
Let us find out the L.C.M of 36,40 and 48
36 = 22 × 32, 40 = 23 × 51, 48 = 24 × 3
∴ LCM = 24 × 32 × 51
= 16 × 9 × 5 = 720
Since 5 has to be the remainder. We have to add 5 to 720 i.e., 720 + 5 = 725
Question 27.
If A = {1, 2, 3} and R = {(1, 1) (1, 2) (2,1) (2, 2) (3, 3)} Prove that R is an equivalence relation on A.
Answer:
R = { (1, 1) (1, 2) (2, 1) (2, 2) (3, 3)}
R is reflexive ∵ (1, 1) (2, 2) (3, 3) ∈ R
R is Symmetric ∵ (1, 2) ∈ R => (2, 1) ∈ R
R is transitive ∵ (1, 2) (2, 1) ∈ R => (1, 1) ∈ R
Question 28.
If a1/3 + b1/3 = c1/3 Prove that (a + b + c)3 = 27 abc.
Answer:
Given a1/3 + b1/3 = -c1/3
Cubing both sides we get
(a1/3 + b1/3)3 = -c
a + b + 3a1/3b1/3(a1/3 + b1/3)3 = -c
a + b + c = -3a1/3, b1/3, c1/3.
Cubing both sides we get
{a + b + c)3 = 27 abc.
Question 29.
Solve: log2 x + log4 x = 3.
Answer:
\(\frac{\log x}{\log 2}+\frac{\log x}{2 \log 2}\) = 3
\(\frac{2 \log x+\log x}{2 \log 2}\) = 3
⇒ 3 log x = 6 log 2 ⇒ log x3 = log 26 ⇒ x3 =(22)3 ⇒ x = 4
Question 30.
The sum of 3 numbers in A.P. is 15 and their product is 105. Find the three numbers.
Answer:
Let the 3 numbers be a – d, a, a + d
Given
![]()
3a = 15 ⇒ a = 5
Also (a – d) (a) (a + d) = 105
5(25 – d2) = 105
25 – d2 = 21 ⇒ 25 – 21 = d2 ⇒ d2 = 4 ⇒ d = 2
The 3 numbers are 5 – 2, 5, 5 + 2 = 3, 5, 7.
Question 31.
The age of a father is 5 times that of a son. 3 years ago the age of the father was 8 times that of his son. Find their present ages.
Answer:
Let the present age of the son be x yrs.
Let the present age of father be 5x yrs.
3yr ago, the age of son is x – 3 and that of father is 5x – 3
Given 5x – 3 = 8 (x – 3)
5x – 3 = 8x – 24
24 – 3 = 8x – 5x = 3x
x = 21 ⇒ x = 7
∴ The present age of son = 7 yrs and father is 35 yrs.
![]()
Question 32.
Solve graphically:
x + 3y ≥ 3; 2x + y ≤ 2; x ≥ 0, y ≥ 0.
Answer:
Let x + 3y = 3,
Put x = 0, y= 1, (0,1)
Put y = 0 x = 0, x = 3, (3,0)
2x + y = 2,
Put x = 0, y = 2, (0,2)
Put y = 0, x = 1, (1, 0)
Plot the two lines in the graph we get
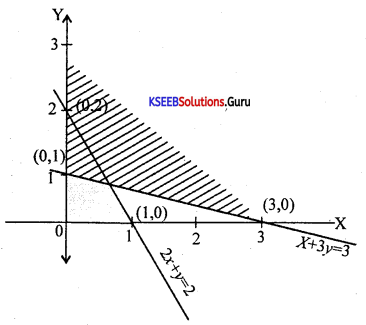
Question 33.
Find the future value of an annuity of 5000 at 12% p.a. for 6 years.
Answer:
F = \(\frac{a\left[(1+i)^{n}-1\right]}{i}\) = 500\(\frac{\left[(1+0.12)^{6}-1\right]}{0.12}\) = 500\(\frac{\left[(1.12)^{6}-1\right]}{0.12}\) = 40575.9 Rs
Future value = 4.575.9
Question 34.
Ritu’s salary was increased by 10% and then again by 5%. If the present salary is ₹ 9,240. What was Ritu’s previous salary?
Answer:
Let his salary be x
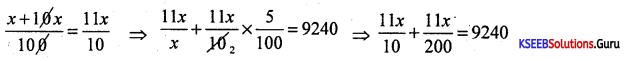
\(\frac{220 x+11 x}{200}\) = 9240 ⇒ 231x = 9240 × 200
x = \(\frac{9240 \times 200}{231}\) = 8000
Question 35.
Prove that \(\frac{1}{1+\cos A}+\frac{1}{1-\cos A}\) = 2cosec2A
Answer:
\(\frac{1}{1+\cos A}+\frac{1}{1-\cos A}\)
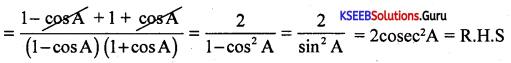
Question 36.
Find area of the quadrilateral whose vertices are A(1, 2) B(6, 2) C(5, 3) and D(3, 4) in order.
Answer:
Area of the Quadrilateral ABCD
= Area of triangle ∆ ABC + Area of ∆ACD
= \(\frac{5}{2}\) + 3 = \(\frac{11}{2}\) sq units
But Area of ∆ABC = \(\frac{1}{2}\)Σx1 (y2 – y3)
= | Area of ∆ABC| + |Area of ∆ACD| = \(\left|\frac{5}{2}\right|\) + |3| = \(\frac{5}{2}\) + 3 = \(\frac{5+6}{2}=\frac{11}{2}\) sq.units
![]()
Question 37.
Find the equation of the locus of the point which moves such that it ¡s equidistant from (4, 2) and x-axis.
Answer:
Let P(x, y) be the point on the locus and A = (4,2)
∴ PA = Y = (PA)2 = y2
⇒ (x – y)2 + (y – 2)2 = y2
![]()
⇒ x2 – 8x – 4y + 20 = 0 is the required equation.
Question 38.
Find k so that the distance from (2, 3) to the line 8x + 15y + k = 0. may be equal to 4 units.
Answer:
\(\left|\frac{8(2)+15(3)+k}{\sqrt{8^{2}+15^{2}}}\right|\) = 4
\(\left|\frac{16+45+k}{\sqrt{64+225}}\right|\) = 4
16 + k = 4\(\sqrt{289}\) = 4 × 17 = 68
k = 4(17) – 61 = 68 – 61 = 7. ∴ k = 1.
Part-D
IV. Answer any SIX questions. (6 × 5 = 30)
Question 39.
In a survey of 100 persons, it was found that 28 read magazine A, 30 read magazine B, 42 read magazine C, 8 need magazines A and B, 10 read magazines A and C, 5 read magazines B and C while 3 read all the three magazines.
Find: (a) How many read none of the three magazines
(b) How many read-only magazines
(c) How many read exactly one magazine only.
Answer:
Given U = 100, n(A) = 28, n(B) = 30, n(C) = 42
n(A∩B) = 8, n(A∩C) = 10, n(B∩C) = 5, n(A∩B∩C) = 3
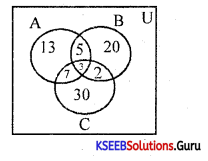
(i) Number of people who read none of the magazines
= 100 – (13 + 5 + 20 + 7 + 3 + 2 + 30)
= 100 – 80 = 20
(ii) No. of people who read only magazines C = 30
(iii) No. of people who read exactly one magazines only = 13 + 20 + 30 = 63
Question 40.
Using log table find the value of \(\frac{21.54 \times 72.6}{6.5}\).
Answer:
Let log = log\(\left(\frac{21.54 \times 72.6}{6.5}\right)\)
logx = log 21.54 + log 72.6 – log 6.5
= 1.3332+ 1.8609-0.8129
x = A.L (2.3812) = 240.58.
Question 41.
Find the sum of all even integers from 40 to 160.
Answer:
Sn = 40, 42, 44……………160
a = 40, d = 2, Tn = 160
Tn = a + (n – 1)d
160 = 40 + (n – 1)2
120 = 2n – 2
122 = 2n ⇒ n = 61
Consider Sn = \(\frac{n}{2}\)(a + l) = \(\frac{61}{2}\)(40+160)= \(\frac{61 \times 200}{2}\) =6100
∴ Sum of all even integers = 6100.
Question 42.
Solve x3 – 10x2 + 29x – 20 = 0. Using synthetic division given that it has an integral root between -3 and 3.
Answer:
f(x) = x3 – 10x2 + 29x – 20
f(1)= 1 – 10 + 29 – 20 = 0
x = 1 is a root of the given equation. Let us remove this root by synthetic division.
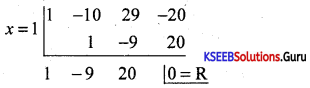
∴ The resulting equation is x2 – 9x + 20 = 0 is the quotient and remainder is 0.
x2 – 9x + 20 = 0 (x – 5) (x – 4) = 0
x = 4 or 5
Thus x = 1, 4, 5 are the roots of the given equation.
Question 43.
The difference between simple interest and compound interest on a certain sum of money invested for 3 years at 6% p.a. is f 110.16. Find the sum.
Answer:
Let the sum = x
S.I = \(\frac{x \times 3 \times 6}{100}\) = 0.18x
C.I. = A – P where A = P(1 + i)n
= x(1 +0.06)3 = 1.191016x
C.I.= A – P = 1.191016x – 1x = 0.191016x
Given C.I. – S.I = 110.16
0.191016x – 0.18x = 110.16
0.011016x = 110.16
x = \(\frac{110.16}{0.011016}\) = 10,000
∴ The sum= 10,000.
Question 44.
Find x if x3 sin45°cos 60° = \(\frac{\tan ^{2} 60^{\circ} \cdot \cos e c 30^{\circ}}{\sec 45^{\circ} \cdot \cot ^{2} 30^{\circ}}\)
Answer:
x3. \(\frac{1}{\sqrt{2}} \cdot\left(\frac{1}{2}\right)^{2}=\frac{(\sqrt{3})^{2} \cdot 2}{\sqrt{2} \cdot\left(\frac{1}{\sqrt{3}}\right)^{2}}\)
x3.\(\frac{1}{\sqrt{2}} \cdot \frac{1}{4}=\frac{3.2}{\sqrt{2} \cdot \frac{1}{3}}\)
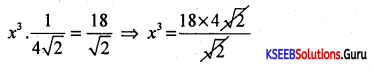
x3. \(\frac{1}{4 \sqrt{2}}=\frac{18}{\sqrt{2}}\) ⇒ x3 = \(\frac{72 \sqrt{2}}{2}\) ⇒ x = 3\(\sqrt{72}\)
Question 45.
Raj wants to invest a lump-sum amount in the bank so that he can get an annual income of Rs.15,000 every year for the next 10 years. If the bank offers 16% p.a. compound interest, what is the amount he should invest today?
Answer:
Given, n = 10yrs, a = 15,000, i = 0.16, P = ?
P = \(\frac{a\left[(1+i)^{n}-1\right]}{i(1+i)^{n}}\)
= \(\frac{15,000\left[(1+0.16)^{10}-1\right]}{0.16(1+0.16)^{10}}=\frac{15,000\left[(1.16)^{10}-1\right]}{0.16 \times(1.16)^{10}}\) = 72498.2
∴ He should invert today 7249.8
Question 46.
A person spent 30% of his wealth and thereafter Rs. 20,000 and further 10% of the remainder. If Rs. 29,250 is still remaining, what was his total wealth?
Answer:
Let his wealth be x Rs
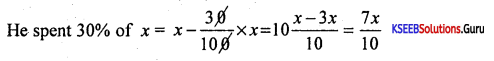
Again he spent 20,000 \(\frac{7 x}{10}\) – 20,000 \(\frac{7 x-2,00,000}{10}\)
Again he spent 10% = \(\left(\frac{7 x-2,00,000}{10}\right)-\frac{7 x-2,00,000}{10} \times \frac{1}{10}\)x
\(\left(\frac{7 x-2 ; 00,000}{10}\right)\left(1-\frac{x}{10}\right)=\frac{(7 x-2,00,000)(10-x)}{100}\)
\(\frac{(7 x-2,00,000)(10-x)}{100}\) = 29,250 =x 75,000
∴ Total wealth = 75,000.
![]()
Question 47.
Prove that A(-3, 6) B(-2,11) C(3,12) and D(2, 7) are the vertices of a rhombus. Also And its area.
Answer:
A(-3, 6) B(-2, 11) C(3, 12) and D(2, 7)
AB = \(\sqrt{(-2+3)^{2}+(11-6)^{2}}=\sqrt{1^{2}+5^{2}}=\sqrt{1+25}=\sqrt{26}\)
BC = \(\sqrt{(3+2)^{2}+(12-11)^{2}}=\sqrt{5^{2}+1^{2}}=\sqrt{25+1}=\sqrt{26}\)
CD = \(\sqrt{(2-3)^{2}+(7-12)^{2}}=\sqrt{(-1)^{2}+(-5)^{2}}=\sqrt{1+25}=\sqrt{26}\)
DA = \(\sqrt{(2+3)^{2}+(7-6)^{2}}=\sqrt{5^{2}+1^{2}}=\sqrt{25+1}=\sqrt{26}\)
d1 = AC\(\sqrt{(3+3)^{2}+(12-6)^{2}}=\sqrt{(6)^{2}+(6)^{2}}=\sqrt{36+36}=\sqrt{72}\) = 6\(\sqrt{2}\)
d2 = BD\(\sqrt{(3+3)^{2}+(12-6)^{2}}=\sqrt{(6)^{2}+(6)^{2}}=\sqrt{36+36}=\sqrt{72}\) = 4\(\sqrt{2}\)
All sides are equal = \(\sqrt{26}\) ∴ ABCD forms Rhombus.
Area = \(\frac{1}{2}\) d1d2 = \(\frac{1}{2}\).6\(\sqrt{2}\).4\(\sqrt{2}\) = 24 sq. units
Question 48.
Find the equation of a straight line passing through the point (2, 2) such that the sum of its intercepts on the axes is 9.
Answer:
Intercept equation is \(\frac{x}{a}+\frac{y}{b}\) = 1
Also given a + b = 9
b = 9 – a
∴ Equation becomes \(\frac{x}{a}+\frac{y}{9-a}\) = 1. But this equation passes through (2,2)
\(\frac{2}{a}+\frac{2}{9-a}\) = 1
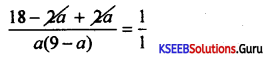
18 = 9a – a2
a2 – 9a + 18 = 0
(a-6) (a-3) = 0
a = 6 or 3,
b = 3 or 6
The required equations are \(\frac{x}{6}+\frac{y}{3}\) = 1 or \(\frac{x}{3}+\frac{y}{6}\) = 1
Part-E
V. Answer any ONE question. (1 × 10 = 10)
(a) If A = {3, 5, 7, 8} B = {4, 5, 7, 9} C = {1, 2, 3, 4, 5}
Find (i) (A – B) × (B – C)
(ii) (A ∩ B) × (B ∩ C)
Answer:
(A – B)= {3, 8}, B – C = {7, 9}
(i) (A – B) × (B – C) = {(3, 7) (3, 9) (8, 7) (8, 9)}
(ii) (A ∩ B) × (B ∩ C) = {5, 7} × {4, 5}
= {5, 4) (5, 5) (7, 4) (7, 5)}.
(b) A manufactures sells his product at Rs. 8.35 per unit, he is able to sell his entire production. His fixed cost is Rs. 2116 and his variable cost per unit is ₹ 7.20 Find
(i) Level of production at which he can make a profit of ₹ 4, 600
(ii) Level of output at which he will incur a loss of ₹1150
(iii) Break-even level of production.
Answer:
C(x)= 7.20x + 2116,
R(x)= 8.35x
P(x) = R(x) – C(x)
(i) P(x) = 4,600,
4600 = 8.35x – [7.20x + 2116] = 1.15x – 2116
1.15x = 4600 + 2116 = 6716 = 5840 .
(ii) C(x) – R(x) = 1150,
7.20x + 2116 – 8.35x = 1150
115x = 966,
x = 840 units
(iii) C(x) = R(x)
720x + 2116 = 8.35x,
2116 = 8.35x – 7.20x
2116 = 1.1 5x
x = 1840 units BEP
(c) Using log find the number of digits in 350.
Answer:
Consider log320 =20 log 3 = 20 × 0.477 1 = 9.542
Since the characteristic is 9, there are 10 digits in 320.
![]()
Question 50.
(a) If the lines 2x – y = 5,
Kx-y = 6 and 4x – y = 1 are concurrent find k.
Answer:
Solving equations 2x – y = 5, & 4x – y = 7 we get

∴ y = 2x – 5 = 2 – 5 = -3
Since lines are concurrent put x = 1 and y = -3 in kx – y = 6
Kx – y = 6 ⇒ K(1) – (-3) = 6
⇒ K + 3 = 6
⇒ K = 6 – 3
⇒ K = 3
(b) Find sum of 7 + 77 + 777 + ……… n terms.
Answer:
Let Sn = 7 + 77 + 777 +…………….n terms
= 7 [1 + 11 + 111 + –—–— to n terms] = \(\frac{7}{9}\)[9 + 99 + 999 + …………. to n terms]
= \(\frac{7}{9}\)[(10 – 1) + (100 – 1) + (1000 – 1)+……………to n terms]
= \(\frac{7}{9}\)[(10 + 102 + 103 +…………to n terms) – (1 + 1 + 1 …………to n terms]
= \(\frac{7}{9}\left[\frac{10\left(10^{n}-1\right)}{10-1}-n\right]\)[… 10 + 102 + 103……….. to n terms is in GP Where a = 10, r = 10]
Sn = \(\frac{7}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)
(c) A scholarship of Rs. 2000 every year has to be instituted. How much should be invested today ¡f the rate of interest, is 8% p.a. .
Answer:
P = \(\frac{a}{i}=\frac{2000}{0.08}\) = 25,000