1st PUC Basic Maths Previous Year Question Paper March 2015 (South)

Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2015 (South), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2015 (South)

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any TEN questions. (10 × 1 = 10)

Question 1.
Write the canonical representation of 360.
Answer:
360 = 2³ × 3² × 5¹

Question 2.
If A= {1, 2, 3, 4} and B = {3, 4, 6} find B -A.
Answer:
B – A = {6}

Question 3.
If f:R→ R is defined by f(x) = x² + 2x – 5. Find f(-1).
Answer:
f (-1) = (-1)² + 2(-1) – 5 = 1 – 2 – 5 = 1 – 7 = – 6

Question 4.
Which is greater?
\(\frac{1}{\left(5^{2}\right)^{3}}\) Or \(\frac{1}{5^{\left(2^{3}\right)}}\)
Answer:
\(\frac{1}{\left(5^{2}\right)^{3}}=\frac{1}{5^{6}}\); \(\frac{1}{5^{2^{3}}}=\frac{1}{5^{8}}\)
\(\frac{1}{\left(5^{2}\right)^{3}}\) is greater than \(\frac{1}{5^{2^{3}}}\)

Question 5.
Evaluate : log_\(\sqrt{3}\)27.
Answer:
Let x = log\(\sqrt{3}\)27
(\(\sqrt{3}\))x = 27 ⇒ 37 = 33 ⇒ \(\frac{x}{2}\) = 3 ⇒ x = 6

Question 6.
Find the sum to infinity of the series :
3, -1, \(\frac{1}{3}\), –\(\frac{1}{9}\) …………………….
Answer:
Sum to infinity = S_∞ = \(\frac{a}{1-r}=\frac{3}{1+\frac{1}{3}}=\frac{3}{\frac{3+1}{3}}=\frac{9}{4}\)

Question 7.
Solve:
Answer:
2(x + 2) = 5(x – 1)
2x + 4 = 5x – 5
4 + 5 = 5x – 2x ⇒ 3x = 9 ⇒ x = 3

Question 8.
Convert 0.12 into a percentage.
Answer:
0.12 × 100= 12%

Question 9.
Define perpetuity.
Answer:
Annuity for ever is called perpetuity
Ex: Endowment prize.

Question 10.
Convert \(\frac{7 \pi}{12}\) into degrees.
Answer:
\(\frac{7 \pi^{\mathrm{c}}}{12}=\frac{7 \times 180}{12}\) = 105°

Question 11.
The average age of 10 boys in a class is 13 years. What is the sum of their ages?
Answer:
X̄ = \(\frac{\sum \mathrm{x}}{\mathrm{n}}\)
13 = \(\frac{\sum \mathrm{X}}{10}\) ⇒ ΣX = 130 years

Question 12.
If the slope of the line is –\(\frac{2}{3}\)find the slope of the perpendicular line to it.
Answer:
Slope of the perpendicular line is \(\frac{3}{2}\)

PART-B

II. Answer any TEN questions: (10 × 2 = 20)

Question 13.
Find the least number which when divided by 6, 10, 15, and 30 leaves no remainder.
Answer:
The least number is nothing but LCM of 6, 10, 15 & 30.

L.C.M = 6 × 5 × 2 × 3 = 180

Question 14.
If X and Y are two sets such that X has 35 elements, (XuY) has 45 elements. How many elements does Y has?
Answer:
n(X) = 35, n(X∪Y) =45, n(Y) = ?
n(X∩Y) = 10
n(X∪Y) = n(X) + n(Y) – n(X∩Y)
45 = 35 + n(Y) – 10
n(Y) = 45 – 25 = 20

Question 15.
If the product of two numbers is 216 and their L.C.M is 36, find their H.C.F.
Answer:
If a × b = 216, L = 36, H = ?
H = \(\frac{\mathrm{a} \times \mathrm{b}}{\mathrm{L}}=\frac{216}{36}\) = 6
∴ HCF = 6

Question 16.
Prove that (x^b-c)^a.(x^b)^c-a.(x^a-b)^c = 1.
Answer:
LHS = x^ab-bc. x^bc-ab. x^ac-bc
= x^{ab-bc+bc-ab+ac-bc}
= x° = 1 = RHS

Question 17.
Insert 4 Arithmetic means between 5 and 10.
Answer:
Let A₁, A₂, A₃, A₄ be the 4 Arithmetic Means between 5 and 10.
∴ 5, A₁, A₂, A₃, A₄, 10 are in A.P.
∴ a = 5, a + 5d = 10 ⇒ 5 + 5d = 10 ⇒ 5d = 5 =* d = 1
∴ A₁ = a + d = 5 + 1= 6
A₂ = a + 2d = 5 + 2 = 7
A₃ = a + 3d = 5 + 3 = 8
A₄ = a + 4d = 5 + 4 = 9

Question 18.
The age of the father is four times that of the son. 5 years ago, the age of the father was seven times that of his son. Find their present ages.
Answer:
Let the present age of the son = x yrs.
5 years ago, the age of the son was x – 5 and that of the father was 4x – 5.
Given 4x – 5 = 7(x – 5)
4x – 5 = 7x – 35
30 = 3x ⇒ x= 10 and 4x = 40
∴ Father’s age is 40 yrs and the son’s age is 10 years.

Question 19.
What principal will amount to Rs? 46,000 in 7 years at 12% p.a.?
Answer:
A = 46, 000, T = 7 yrs , R = 12% •
A = P(1 + \(\frac{\mathrm{TR}}{100}\))
46000 = P(1 + 7 × 0.12)
P = \(\frac{46000}{1+0.84}=\frac{46000}{1.84}\) = 25000
P = 25,000

Question 20.
Solve for x, if 7x + 3 < 5x + 9, x in R and represent the solution on the number line.
Answer:
7x + 3 < 5x + 9
2x < 6
x < 3

Question 21.
The average score of 35 girls is 80 and the average score of 25 boys is 68. Find the average score of both boys and girls together.
Answer:
X̄₁₂ = \(\frac{35 \times 80+25 \times 68}{35+25}=\frac{2800+1700}{60}=\frac{4500}{60}\) = 75
∴ Average score of both is 75.

Question 22.
By selling 8 erasers a trader gains the selling price of 1 eraser. Calculate the gain percent.
Answer:
Let the S.R of one eraser be x.
∴ the SP of 8 erasers = 8x
profit = x
C.P = S.P – Profit = 8x – x = 7x
Profit % = \(\frac{\text { Profit }}{\text { C.P }}\) × 100 = \(\frac{\mathrm{x}}{7 \mathrm{x}}\) × 100 = 14\(\frac{2}{7}\)%

Question 23.
Prove that : \(\sqrt{\frac{1+\cos A}{1-\cos A}}\) = cosecA + cotA
Answer:
LHS = \(\sqrt{\frac{1+\cos A}{1-\cos A}}=\sqrt{\frac{(1+\cos A)^{2}}{1-\cos ^{2} A}}=\sqrt{\left(\frac{1+\cos A}{\sin A}\right)^{2}}=\frac{1}{\sin A}+\frac{\cos A}{\sin A}\) = cosecA + cosA = RHS

Question 24.
Evaluate: sin2\(\frac{\pi}{6}\) + cos2 \(\frac{\pi}{3}\) – tan2\(\frac{\pi}{4}\) + cot2\(\frac{\pi}{4}\)
Answer:
(sin 30)² + (cos 60)² – (tan 45)² + (cot 45)²
= \(\left(\frac{1}{2}\right)^{2}+\left(\frac{1}{2}\right)^{2}\) – 12 + 12
= \(\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

Question 25.
Using the concept of the slope, show that the points (-4, -5), (1, -1) and (6, 3) are collinear.
Answer:
Slope of AB = slope of AC
\(\frac{-1+5}{1+4}=\frac{3+5}{6+4}\)
\(\frac{4}{5}=\frac{8}{10}\)
⇒ slopes are equal
∴ the points are collinear.

PART-C

II. Answer any TEN questions: (10 × 3 = 20)

Question 26.
In a survey of 5000 persons, it was found that 2800 read Indian Express and 2300 read Deccan Herald while 400 read both. How many read either Indian Express nor Deccan Herald?
Answer:
n(I) = 2800, n(D) = 2300, n(ID) = 400

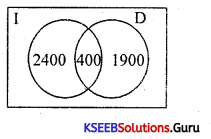
n(I∪D) = n(I) + n(D) + n(I∩D)
= 2800 + 2300 – 400
= 4700
∴ 5000 – 4700 = 300 will read either Indian Express nor Deccan Herald.

Question 27.
Show that the relation “is congruent to” is an equivalence relation on a set T of triangles.
Answer:
Any ∆ T₁ is congruent to itself ∴ R is reflexive.
If a ∆T₁ is congruent to ∆ T₂ then T₂ is congruent to T₁. ∴ R is symmetric.
If a ∆T₁ is congruent to ∆ T₂ & ∆T₂ is congruent to ∆ T₃ then ∆T₁ is congruent to ∆ T₃ ∴ R is transitive.
Since R is reflexive, symmetric, and transitive. Hence it is an equivalence relation.

Question 28.
Prove that : log₄8.log₂32.log₁₆4 = \(\frac{15}{4}\)
Answer:
L.H.S = \(\frac{\log 8}{\log 4} \times \frac{\log 32}{\log 2} \times \frac{\log 4}{\log 16}=3 \log 2 \times \frac{5 \log 2}{\log 2} \times \frac{1}{4 \log 2}=\frac{15}{4}\)

Question 29.
Solve : 2^2x – 6.2^x + 8 = 0
Answer:
(2x)² – 6.2^x + 8 = 0
Put y = 2x
y² – 6y + 8 = 0
(y – 2)(y – 4) = 0 ⇒ y = 2 or y = 4
2^x = 2¹ or 2^x = 2² ⇒ x = 1 or x = 2

Question 30.
Find the sum to n terms of the GP. 7 + 77 + 777 +………………..
Answer:
Let S = 7 + 77 + 777 +………………+ n terms
\(\frac{\mathrm{S}}{7}\) = 1 + 11 + 111 +…………..n terms
\(\frac{9 \mathrm{~S}}{7}\) = 9 + 99 + 999 +……………n terms
\(\frac{9 \mathrm{~S}}{7}\) = (10 – 1) + (100 – 1) + (1000 – 1) +………………… n terms
\(\frac{9 \mathrm{~S}}{7}\) = (10 +100 + 1000 + …………….n terms) – (1 + 1 + ………………n terms)
\(\frac{9 \mathrm{~S}}{7}\) = (10+100 + 1000 + …………….n terms) – (1 + 1 +………………. n terms)
= \(\frac{10\left(10^{n}-1\right)}{9}\) – n
S = \(\frac{7}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)

Question 31.
Divide ₹ 110 into two parts so that 5 times of one part together with 6 times of other parts will be equal to Rs. 610.
Answer:
Let x & y be the two parts.
Then the number will be x + y
Given: x + y = 110 …………(1)
Also given 5x + 6y = 610 ……………….(2)
Solving (1) and (2) we get x = 50 & y = 60
Hence the two parts of 110 are ₹ 50 and ₹ 60.

Question 32.
Solve the following inequalities graphically :
x + 3y > 3
2x + y > 2
x > 0, y > 0
Answer:
Consider x + 3y = 3
Put x = 0, y = 1 (0,1)
put y = 0, x = 3(3, 0)

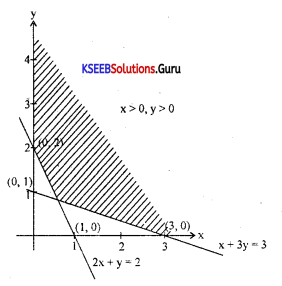
Let 2x + y = 2
Put x = 0, y = 2 (0, 2)
Put y = 0, x = 1 (1,0)

Question 33.
Find the present value of an annuity due of Rs. 8,000 for 5 years at 5% p.a.
Answer:
The present value of an annuity due is.
P = \(\frac{\mathrm{A}\left((1+\mathrm{i})^{\mathrm{n}}-1\right)(1+\mathrm{i})}{\mathrm{i}(1+\mathrm{i})^{n}}=\frac{8000\left[(1+0.05)^{2}-1\right](1+0.05)}{(0.05)(1+0.05)^{5}}\) = ₹ 36,369.50

Question 34.
Find the ratio in which the line joining the points (3, 5) and (-7, 9) is divided by the point.
Answer:
A = (3, 5) B = (-7, 9)
P(x, y) = (\(\frac{1}{2}\), 6)
The ratio m : n on which P divides AB is given by
\(\frac{\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{x}-\mathrm{x}_{1}}{\mathrm{x}_{2}-\mathrm{x}}=\frac{\frac{1}{2}-3}{-7-\frac{1}{2}}=\frac{1-6}{-14-1}=\frac{-5}{-15}=\frac{1}{3}\)
∴ \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{1}{3}\) ⇒ m: n = 1: 3
∴ P divides AB in the ratio 1 : 3 internally.

Question 35.
A dealer buys 200 quintals of wheat at Rs. 1,200 a quintal. He spends Rs. 10,000 on transportation and storage. He sells the wheat at Rs. 13 per kg. Find his profit or loss. Also, calculate it as a percentage.
Answer:
Cost Price of 200 quintals of wheat = 1200 × 200 = 2,40, 000
Transportation and storage cost = Rs. 10,000
Total C. P = 2,40,000 + 10,000 = 2,50,000
Total S. P = 13 × 20000 = 2,60,000
Profit = 2,60,000 – 2,50,000 = 10,000
Profit% = \(\frac{\text { Profit }}{\mathrm{CP}}\) × 100 = \(\frac{10,000}{2,50,000}\) × 100 = 4%

Question 36.
If sin θ = \(\frac{-3}{5}\) and lies in IV quadrant, then prove that \(\frac{3 \tan \theta-4 \cos \theta}{4 \tan \theta+3 \cos \theta}=\frac{109}{12}\)
Answer:
sin θ = \(\frac{-3}{5}\), cos θ = \(\frac{4}{5}\), tan θ = \(\frac{-3}{4}\)
LHS = \(\frac{3 \tan \theta-4 \cos \theta}{4 \tan \theta+3 \cos \theta}=\frac{3 \cdot\left(-\frac{3}{4}\right)-4\left(\frac{4}{5}\right)}{4\left(-\frac{3}{4}\right)+3\left(\frac{4}{5}\right)}=\frac{-\frac{9}{4}-\frac{16}{5}}{-\frac{12}{4}+\frac{12}{5}}=\frac{-\frac{45-64}{20}}{\frac{-60+48}{20}}=\frac{-109}{-12}=\frac{109}{12}\) = RHS

Question 37.
Show that the points (4,4) (3,5) and (-1, -1) are the vertices of a right-angled triangle.
Answer:
A = (4, 4) B = (3, 5) C = (-1,-1)
AB = \(\sqrt{(3-4)^{2}+(5-4)^{2}}=\sqrt{(-1)^{2}+1^{2}}=\sqrt{2}\)
AB² = 2 …………….(1)
BC = \(\sqrt{(-1-3)^{2}+(-1-5)^{2}}=\sqrt{(-4)^{2}+(-6)^{2}}=\sqrt{16+36}=\sqrt{52}\)
BC² = 52 ……………..(2)
CA = \(\sqrt{(-1-4)^{2}+(-1-4)^{2}}=\sqrt{(-5)^{2}+(-5)^{2}}=\sqrt{25+25}=\sqrt{50}\)
CA² = 50 …………………(3)
From 1, 2 and 3 we get
AB² + CA² = BC²
∴ A, B & C form a right angled triangle.

Question 38.
Find the equation of the straight line which passes through the point of intersection of 2x-3y = 4 and 2x + 2y = 1 and perpendicular to the line x + 4y = 8.
Answer:
Solving 2x – 3y = 4………………(1)
2x + 2y = 1 ……………(2)
We get x = \(\frac{11}{10}\) & y = –\(\frac{3}{5}\)
Any line perpendicular to x + 4y = 8 is of the form 4x -y + k = 0. But this line passes through \(\)
4.\(\left(\frac{11}{10},-\frac{3}{5}\right)\) + k = 0
\(\frac{11}{10}-\left(-\frac{3}{5}\right)\) = -K
-K = \(\frac{25}{5}\) = 5 ⇒ k = -5
The required equation of the line is 4x – y – 5 = 0

PART-D

IV. Answer any SIX questions : (6 × 5 = 30)

Question 39.
In a survey of 100 persons, it was found that 28 read magazine A, 30 read magazine B, 42 read magazine C, 5 read magazine B and C, while 3 read all three magazines. Find
(i) How many read one of the three magazines?
(ii) How many read-only magazines C?
Answer:
Given U = 100, n(A) = 28, n(B) = 30, n(C) = 42,
n(A∩B) = 8, n(A∩C) = 10, n(B∩C) = 5

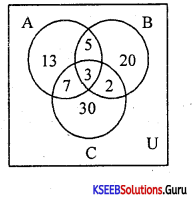
n(A∩B∩C) = 3
(i) Number of people who read some of the magazines
= 100 – (13 + 5 + 20 + 7 + 3 + 2 + 30)
= 100 – 80 = 20
(ii) Number of people who read the only magazine C = 30.

Question 40.
Find the sum of all numbers between 50 and 200 which are divisble by 11.
Answer:
AP is given by
55, 66, 77…………………198
Here a = 55, l = T = 198 d= 11
Tn = a + (n – 1)d
198 = 55 + (n – 1) 11
198 – 55 = (n – 1)11
143 = (n – 1)11
(n – 1) = \(\frac{143}{11}\) = 13
n= 13 + 1 = 14
∴ n = 14
S_n= \(\frac{\mathrm{n}}{2}\)(a + l) = \(\frac{14}{2}\)(55 + 198) = 7(253) = 1771
∴ Sum = 1771

Question 41.
If there is an integral root between -3 and +3, by inspection and then by using synthetic division solve x³ +15x² – 72x + 76 = 0
Answer:
Given x³ + 15x² -72x + 76 = 0
x = 2 is the multiplier.

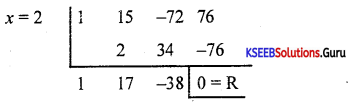
∴ Quotient is x2 + 1 7x – 38 = 0
Solving this we get (x + 19)(x – 2) = 0
x = -19, 2
∴ the roots of the given equation are 2, 2, -19

Question 42.
If ₹ 9,000 amounts to Rs. 10,418.625 in 3 years, And the compound interest rate present. .
Answer:
Given P = 9000, A= 10,418.625 .
n = 3 yrs,, r = ?
r = A.L\(\left\{\frac{\log A-\log P}{n}\right\}\) -1 = r = A.L\(\left\{\frac{\log 10418.625-\log 9000}{3}\right\}\) – 1 = A.L[0.021067] – 1 = 1.050 – 1 = 0.05
∴ r = 0.05 x 100 = 5%

Question 43.
Preritha wants to buy a house after 5 years when it is expected to cost Rs. 50 lakhs. How much should she save annually if her savings earn a compound interest of 12% p.a?
Answer:
Given: F = 50,00,000; n = 5, i = 0.12
F = \(\frac{A\left[(1+i)^{n}-1\right]}{i}\)
50,00,000 = A(6.3528)
A = \(\frac{50,00,000}{6.3528}\)
∴ A = ₹ 787054.5

Question 44.
Find the equations of the medians of the triangle formed by the points (-1, 3), (-3, 5), and (7, -9).
Answer:
Let D as the midpoint of BC = \(\left(\frac{-3+7}{2}, \frac{5-9}{2}\right)\)
Equation of the median AD is
\(\frac{y-y_{1}}{x-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac{y-3}{x+1}=\frac{-2-3}{2+1}=\frac{-5}{3}\)
3y – 9 = -5x – 5
5x + 3y – 4 = 0

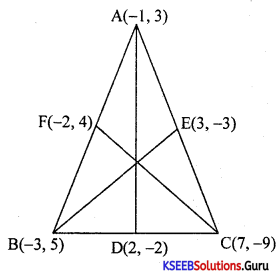
Let E is the mid-point of AC = \(\left(\frac{-1+7}{2}, \frac{3-9}{2}\right)\) = (3, 3)

The equation of the median BE is
\(\frac{y-5}{x+3}=\frac{-3+5}{3+3}=\frac{-8}{6}=\frac{-4}{3}\)
3y – 15 = -4x – 12
4x + 3y – 3 = 0

Let F is the midpoint of AB = \(\left(\frac{-1-3}{2}, \frac{3+5}{2}\right)\) = (-2, 1)
The equation of the median CF is
\(\frac{y+9}{x-7}=\frac{-9+4}{7+2}=\frac{-13}{9}\)
9y + 81 = -13x + 91
13x + 9y – 10 = 0

Question 45.
Evaluate: \(\frac{213.781 \times 7.434}{6.321}\) using logarithmic tables.
Answer:
Let x = \(\frac{213.781 \times 7.434}{6.321}\)
logx = log\(\left[\frac{213.781 \times 7.434}{6.321}\right]\)
logx = log213.781 + log7.434 – log6.321
= 2.3298 + 0.87 12 – 0.8008
= 2.4002
x = A.L (2.4002) = 251.3

Question 46.
Find the foot of the perpendicular drawn from the point (-2, -1) on the line 3x + 2y – 5 = 0.
Answer:
Let P(x,y) = (-2, -1), Q (h, k) be the foot of the perpendicular on the line 3x + 2y – 5 = 0
\(\frac{\mathrm{h}-x_{1}}{\mathrm{a}}=\frac{\mathrm{k}-\mathrm{y}_{1}}{\mathrm{~b}}=\frac{-\left(\mathrm{ax}_{1}+\mathrm{by}_{1}+\mathrm{c}\right)}{\mathrm{a}^{2}+\mathrm{b}^{2}}\)

Here a = 3, b = 2, c = 5 & (x₁, y₁)(-2, -1) .
Substituting all these values in the above expression we get
\(\frac{h-(-2)}{3}=\frac{k-(-1)}{2}=-\left(\frac{3(-2)+2(-1)-5}{3^{2}+2^{2}}\right)\)
\(\frac{h+2}{3}=\frac{k+1}{2}\) = -(-1) = 1
\(\frac{h+2}{3}\) = 1 if \(\frac{\mathrm{k}+1}{2}\) = 1
h = 1, k = 1
The foot of the perpendicular is Q (1, 1).

Question 47.
If x = arsin AcosB, y = brsin AsinB and z = crcosA , prove that \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}\) = r²
Answer:
Given x = arsin AcosB ; y = brsinASinB; z = crcosA
L.H.S. = \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}\)
= \(\frac{a^{2} r^{2} \sin ^{2} A \cos ^{2} B}{a^{2}}+\frac{b^{2} r^{2} \sin ^{2} A \sin ^{2} B}{b^{2}}+\frac{c^{2} r^{2} \cos ^{2} A}{c^{2}}\)
= r² sin² A (cos² B + sin² B) + r² cos2 A
= r² sin² A.1 + r² cos² A = r² (sin² A + cos² A) = r².1 = r² = R.H.S.

Question 48.
Find the equation of the locos of a point that moves such that its distance from the point (-4, 0) is 4 times its distance from (0, -2).
Answer:
Let P(x,y) be any point on the locus
A = (-4, 0) B = (0, -2)
Given PA = 4PB PA² = 16PB²
(x + 4)²+(y-0)² = 16[(x-0)²+(y + 2)²]
x² + 16 + 8x + y² = 16[x² + y² + 4 + 4y]
16x²+ 16y²+ 64 + 64y = x² + y² + 8x +16
15x² + 15y² – 8x + 64y + 48 = 0 is the required equation of the locus. ‘

PART-E

V. Answer any ONE question : (6 × 5 = 30)

Question 49.
(a) Find the equation of a line passing through (-2, 6) and the sum of intercepts on the coordinate axis is 5.
Answer:
Let x-intercept = a, y-intercept = b
Given: a + b = 5
The equation of the line is \(\) = 1
x(5 – a) + y(a) = a(5 – a).
But this passes through the point (-2, 6)
-2(5 – a) + 6a = 5a – a²
-10 + 2a + 6a = 5a – a²
a² – 3a – 10 = 0
(a – 5)(a + 2) = 0
a = 5 or a = -2
If a = 5 then b = 5 – 5 = 0,
If a = -2, b = 5 – (-2) = 7
the required equations of the lines are
\(\frac{x}{-2}+\frac{y}{7}\) = 1
7x – 2y = -14
or 7x – 2y + 14 = 0

(b) Evaluate : \(\frac{\sin 150^{\circ}-5 \cos 300^{\circ}+7 \tan 225^{\circ}}{\tan 135+3 \sin 210^{\circ}}\)
Answer:
\(\frac{\sin 150-5 \cos 300+7 \tan 225}{\tan 135+3 \sin 210}=\frac{\sin (180-30)-5 \cos (360-60)+\tan (180+45)}{\tan (180-45)+3 \sin (180+30)}\)
= \(\frac{\sin 30-5 \cos 60+7 \tan 45}{-\tan 45-3 \sin 30}=\frac{\frac{1}{2}-5 \cdot \frac{1}{2}+7.1}{-1-\frac{3}{2}}=\frac{\frac{1-5+14}{2}}{\frac{-2-3}{2}}=\frac{10}{-5}\) = -2

(c) If log6 = 0.7782, find the number of zeroes between the decimal point and the first significant figure in (0.6)30.
Answer:
Let x = (0.6)30
logx = 30log0.6
= 30 × 1.7782 = 30 (-1 + 0.7782)
= -30 + 23.346
= -7̄.346
= 7̄.346
Since the characteristic is 7̄. Hence the required number of zeros is 6.

Question 50.
(a) Three numbers whose sum is 12 are in A.P. If 1, 4, 11 are added to them the resulting numbers are in G.P. Find the numbers.
Answer:
Let the 3 numbers be a – d, a, a + d
By data a-d + a + a + d = 12
3a = 12 ⇒ a = 4
Also by data 4-d + 1, 4 + 4, 4 + d + 11 are in G.P.
5 – d, 8, 15 + d are in G.P.
∴ \(\frac{8}{5-d}=\frac{15+d}{8}\)
64 = (5 – d)(15 + d)
64 = 75 + 5d – 15d – d².
d² + 10d – 11 = 0
(d + 11 )(d – 1) = 0
d = 1 and d = -11
When a = 4, d = 1 the required numbers are 3, 4, 5
When a = 4, d = -11 then required numbers are 15, 4, -7.

(b) A watch manufacturer produced 100 watches for a total cost of Rs. 20,000 and when the production is increased to 200 watches the total cost increases to Rs. 30,000. Assuming that the costs and outputs are linearly related, find the cost equation and find the cost of manufacturing 150 watches.
Answer:
Total cost = TVC + TFC
C(x) = ax + b
When x = 100 watches
C(x) = 100a + b
20,000 = 100a + b ……………(1)
Similarly when x = 200 watches
30,000 = 200a + b. ……………..(2)
Solving equations 1 and 2 we get
100a = 10,000
10,000
∴ a = \(\frac{10,000}{100}\) = 100
20,000 = 100 × 100 + b
∴ b = 20,000 – 10,000 = 10,000
∴ when x = 150, T.C 100 × 150 + 10,000
TC = ₹ 25,000

(c) Form the cubic equation whose roots are -1, 4, 6.
Answer:
The cubic equation with the roots -1, 4 & 6 is given by
(x + 1)(x – 4)(x – 6) = 0