Students can Download 1st PUC Basic Maths Previous Year Question Paper March 2015 (North), Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Previous Year Question Paper March 2015 (North)
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any TEN questions. (10 × 1 = 10)
Question 1.
Write the canonical representation of 156.
Answer:
22 × 31 × 131
Question 2.
If A = {1, 2, 3, 4, 5} and relation R on A is defined as R = {(x, y) : x = y}, find R.
Answer:
R = {(1, 1), (2,2), (3, 3), (4,4), (5, 5)}
Question 3.
If f is a function defined by f(x) = 3x + 5, find f(3).
Answer:
f(3) = 3 × 3 + 5 = 14
Question 4.
Simplify : ax+y a2x-y
Answer:
ax+y.a2x-y = ax+y+2x-y = a3x
![]()
Question 5.
Express 3-2 = \(\frac{1}{9}\) in logarithmic form.
Answer:
-2 = log3(\(\frac{1}{9}\))
Question 6.
Find the 30th term of the A.P. 2, 5, 8,………………….
Answer:
T30 = 2 + 29 × 3 = 2 + 87 = 89
Question 7.
Solve for x : 2(7 + x) – 10 = 16 – 2(x – 24).
Answer:
14 + 2x – 10 = 16 – 2x + 48 = 4x = 68 ⇒ x = 17
Question 8.
Find the present value of a perpetuity of ₹ 3,000 to be received forever at 4% p.a.
Answer:
P80 = \(\frac{A}{r}=\frac{3000}{0.04}\) = ₹ 75,000
Question 9.
The average score of 20 boys is 60% and the average score of 30 girls is 70%. Find their combined average score.
Answer:
X̄12 = \(\frac{20 \times 60+30 \times 70}{20+30}\) = 66%
Question 10.
Convert 0.32 into percentages.
Answer:
0.32 × 100 = 32.00 = 32%
![]()
Question 11.
Express \(\frac{3 \pi}{5}\) in degree measure.
Answer:
\(\frac{3 \pi}{5}=\frac{3 \times 180}{5}\) = 108
Question 12.
Find the distance of the point (5,4) from the origin.
Answer:
Distance = \(\sqrt{5^{2}+4^{2}}=\sqrt{25+16}=\sqrt{41}\)
PART-B
II. Answer any TEN questions : (10 × 2 = 20)
Question 13.
Find the sum of all positive divisors of 34 × 53 × 72.
Answer:
Sum of all positive divisors = T(n) ∴ T(n) = (4+ 1)(3 + 1)(2+ 1) = 60
Question 14.
Find the number which when divided by 16, 20, and 40 leaves the same remainder 4.
Answer:
L.C.M of the given numbers 16,20 & 40 is 80 ∴ the required number = 80 + 4 = 84
Question 15.
If A = (1, 3, 5}, B{5}, C = {7}, find A × (B – C)
Answer:
B – C = {5}
A × (B – C) = {1, 3, 5} × {5} = {(1,5) (3,5) (5,5)}
Question 16.
Simplify: \(\frac{2^{\left(2^{0}\right)}+\left(2^{0}\right)^{3}}{\left(2^{3}\right)^{2}+\left(2^{2}\right)^{0}}\)
Answer:
\(\frac{2^{\left(2^{0}\right)}+\left(2^{0}\right)^{3}}{\left(2^{3}\right)^{2}+\left(2^{2}\right)^{0}}=\frac{2^{1}+1^{3}}{8^{2}+1}=\frac{2+1}{64+1}=\frac{3}{65}\)
![]()
Question 17.
Insert 3 geometric means between -4 and 64.
Answer:
Let g1, g2, g3 are G.Ms. ∴ -4. g1, g2, g3, -64 are in G.P.
Here a = -4, ar4 = -64 ⇒ r4 = \(\frac{-64}{-4}\) = 16 = 24 ⇒ r = 2
the 3 G.Ms are g1 = ar = -8; g2 = ar2 = -16; g3 = ar3 = -32
Question 18.
Solve by formula method : 5x2 – 7x – 12 = 0
Answer:
x = \(\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}\)
a = 5, b = -7, c = -12.
x = \(\frac{7 \pm \sqrt{(-7)^{2}-4(5)(-12)}}{10}=\frac{7 \pm \sqrt{49+240}}{10}=\frac{7 \pm \sqrt{289}}{10}=\frac{7 \pm \sqrt{17^{2}}}{10}=\frac{7 \pm 17}{10}\)
∴ x = \(\frac{12}{5}\), -1
Question 19.
Solve 3x – 2 < 2x + 1, x ∈ R and represent on the number line.
Answer:
3x – 2 < 2x + 1
3x – 2x < 1 + 2
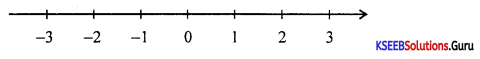
x < 3
Question 20.
What sum will amount to ₹ 46,000 in 7 years at 12% p.a. SI?
Answer:
A = P(1 + \(\frac{\mathrm{TR}}{100}\))
P = \(\frac{A}{\left(1+\frac{T R}{100}\right)}=\frac{46,000}{\left(1+\frac{7 \times 12}{100}\right)}\) = ₹ 25,000
Question 21.
The average height of a group of people is 6 ft. 10 more people with an average height of 5 ft. join the group. Find the average height of the new group of 60 people.
Answer:
Total height of 50 people = 50 × 6 = 3 00
Total height of 10 people = 10 × 5 = 50
Total height of 60 people = 300 + 50 = 350
Hence new average = \(\frac{350}{60}\) = 5.83 ft.
Question 22.
While taking measurement, a tailor writes 34 instead of 24. What is the percentage error?
Answer:
Error = 34 – 24 = 10
∴ Error percent = \(\frac{10}{24}\) × 100 = 41.6%
Question 23.
Find (1 + tan2θ)(1 – sin2θ) = 1
Answer:
LHS = (1 + tan2θ)(1 – sin2θ) = sec2θ.cos2θ = \(\frac{1}{\cos ^{2} \theta}\) .cos2θ = 1 = RHS
Question 24.
Find the small value of : cos60°- sin30° – cot3345°
Answer:
cos60 – sin30 – cot3(45°) = \(\frac{1}{2}-\frac{1}{2}\) – (1)3 = -1
![]()
Question 25.
Find k if the lines 2x – 3y + 4 = 0 and x + ky = 3 are perpendicular.
Answer:
m1 = \(\frac{-a}{b}=\frac{2}{3}\)
m2 = \(\frac{-1}{K}\).
∵ lines are perpendicular .. m1 × m, = -1
⇒ \(\frac{2}{3} \times \frac{-1}{\mathrm{k}}\) = -1
⇒ \(\frac{2}{3} \times \frac{-1}{k}\) = -1
⇒ k = \(\frac{2}{3}\)
PART-C
III. Answer any TEN questions: (10 × 3 = 20)
Question 26.
Find the HCF of \(\frac{8}{9}, \frac{32}{81}, \frac{16}{27}\)
Answer:
H.C.F of 8, 32, 16 = 8
L.C.M of 9, 81, 27 = 81
∴ Required HCF = \(\frac{\text { HCF of N.R }}{\text { LCM of DNR }}=\frac{8}{81}\)
Question 27.
If f(x) = x2 g(x) = x + 1, find the value of
(i) fog(1) (ii) gof(1) and (iii) fof(2)
Answer:
(i) fog(1) = f(g(1)) = f(1 + 1) = f(2) = 22 = 4.
(ii) gof(1) = g(f(1)) = g(12) = g(1) = 1 + 1 = 2
(iii) fof(2) = f(f(2)) f(22) = f(4) = 42 = 16
Question 28.
If A = {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8}, then verify Au(BnC) = (Au B)n(AuC)
Answer:
A∪ B = {1, 2, 3,4, 5, 6}
A∪ C = {1, 2,3,4, 5, 6, 7, 8}
B∩ C= {4,5, 6}
A∪(B∩C) = [1,2,3,4,5,6] = LHS
(A∪B)∩(A∪C) = {1,2,3,4,5,6} = RHS
∴ LHS = RHS
Question 29.
If x = log, 9, y = log, 7, z = log, 4 then show that xyz = 2.
Answer:
LHS = xyz = \(\frac{\log 9}{\log 2} \times \frac{\log 7}{\log 9} \times \frac{\log 4}{\log 7}=\frac{\log 2^{2}}{\log 2}=2 \frac{\log 2}{\log 2}\) = 2 = RHS
Question 30.
The sum of 3 numbers in an AP is 15 and their product is 105. Find the numbers.
Answer:
Let the 3 numbers be (a – b), a, (a + d)
Given sum =15
⇒ a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
Product =105
⇒ (a-d)(a)(a + d) = 105
⇒ d = ±2
∴ The three numbers are 3, 5, 7
![]()
Question 31.
Solve x3 + 6x2 + 9x + 4 = 0 using synthetic division, given that it has an integral root between -3 and 3.
Answer:
x = -1 is a root of the equation x3 + 6x2 + 9x + 4 = 0
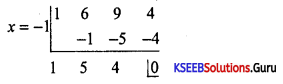
Using synthetic division and getting the reduced equation as x2 + 5x + 4 = 0 solving we get
x = -1 & x = -4
Question 32.
Solve the system of linear inequalities graphically : x + y < 6 and x + y > 4.
Answer:
Consider x + y = 6, x + y = 4
x = 0, y = 6 ⇒ (0,6) (0,4)
y = 0, x = 6 ⇒ (6,0) (4,0)
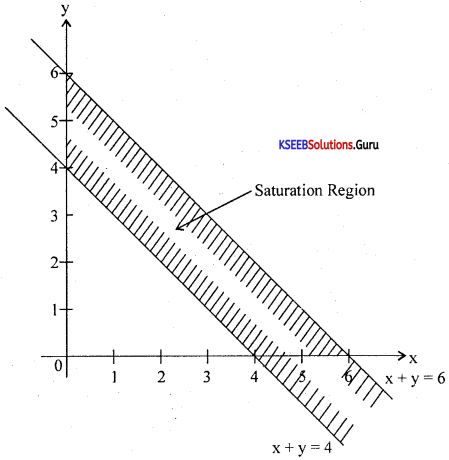
Question 33.
The cost of a refrigerator is ₹ 27,000. If it depreciates at the rate of 8% p.a., find its value after 4 years.
Answer:
A = 27,000(1 -0.08)4 = 27,000(0.02)4= ₹19,342.61
Refrigerators value after 4 years = 19,342.61
Question 34.
10 years ago, the average age of a family of 4 was 24 years. 2 children have been born and the average age remains the same. What are the present ages of the 2 children if their ages differ by 2 years?
Answer:
Let the total age of 4 members = 96 = 4 × 24
After 10 years total age of 4 = 96 + 40 = 136
Let Ages of 2 children x & x + 2.
∴ Total age of 6 = 136 + x + x + 2 = 138 + 2x
Given average age = 24 ⇒ \(\frac{138+2 x}{6}\) = 24 ⇒ x = 3
∴ Ages of 2 children = 3 & 5 years
Question 35.
Ritu’s salary was increased by 10% and then again by 5%. If the present salary is ₹ 9,240, then what was her previous salary?
Answer:
Let the original salary – x
With 10% increase, salary = x + 0.1x = 1.1x
with 5% increase, salary = 1.155x
1.155x = 9240
⇒ x = \(\frac{9240}{1.155}\) = ₹ 8,000
![]()
Question 36.
If cosecθ = and 90° < θ < 1800, then prove that \(\frac{4 \sin \theta-7 \cos \theta}{3 \sin \theta+2 \cos \theta}\) = 40
Answer:
sinθ = \(\frac{3}{5}\) cosθ = \(\frac{-4}{5}\)
(∵ in II quadrant cosθ is negative)
LHS = \(\frac{4 \sin \theta-7 \cos \theta}{3 \sin \theta+2 \cos \theta}=\frac{4 \cdot \frac{3}{5}-7\left(-\frac{4}{5}\right)}{3 \cdot \frac{3}{5}+2 \cdot\left(\frac{-4}{5}\right)}=\frac{\frac{12}{2}+\frac{28}{5}}{\frac{9}{5}-\frac{8}{5}}=\frac{\frac{40}{5}}{\frac{1}{5}}\) = 40 = RHS
Question 37.
3 consecutive vertices of a parallelogram are A (3, 0), B(5, 2), and C (-2, 6). Find the fourth vertex.
Answer:
Let D(x, y) be the fourth vertex
w.k. that in a parallelogram diagonal bisect each other
∴ midpoints are equal.
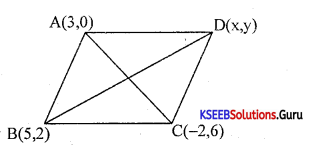
\(\left(\frac{x+5}{2,}, \frac{y+2}{2}\right)=\left(\frac{3-2}{2}, \frac{0+6}{2}\right)\)
⇒ x + 5 = 1, y + 2 = 6
⇒ x = -4, y = 4
∴ the fourth vertex is D(-4, 4)
Question 38.
Derive the slope-intercept form of a straight line.
Answer:
Required equation is y = mx + c
PART-D
IV. Answer any SIX questions : (6 × 5 = 30)
Question 39.
In a class of 50 students, 15 do not participate in any games, 25 play cricket, and 20 play football. Find the number of students who play both. Represent the results using the Venn diagram.
Answer:
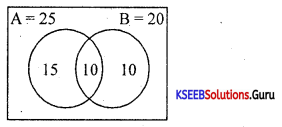
n(A∪B) = 50-15 = 35
n(A ∩ B) = n(A) + n(B) – n(A ∪ B)
n(A∩B) = 25 + 20-35 = 10
Question 40.
Evaluate using log tables : \(\frac{5.634 \times 25.64}{12.72}\)
Answer:
logx = log\(\left(\frac{5.634 \times 25.64}{12.72}\right)\)
= log 5.634 + log 25.64 – log12.72
logx = 0.7508+ 1.4089-1.1044
x = A.L (1.0553)
x = 11.36
Question 41.
Find the sum of all integers between 60 and 400 which are divisble by 13.
Answer:
S = 65, 78, 91 ……………………390
a = 65, d = 13, Tn = 390, n = ?, S =?
Tn = a + (n – 1)d
390 = 65 + (n- 1)13 ⇒ n = 26
Sn = \(\frac{n}{2}\)(a + l) = \(\frac{26}{2}\)(65 + 390) ⇒ Sn = 5915
![]()
Question 42.
A certain two-digit number is 4 times the sum of the digits. If 18 is added to the number, the digits get interchanged. Find the number.
Answer:
Let x be in 10th place, y in units place
∴ the number = 10x + y
Given 10x + y = 4 (x + y)
⇒ y = 2x…………………(1)
Also 10x + y + 18 = 10y + x
⇒ x + 2 = y……………….(2)
Solving (1) and (2) we get
2x = x + 2 ⇒ x = 2
∴ x = 2 & y = 4
Hence required number = 24.
Question 43.
Find the Cl on ₹ 7500 at 14% for 14 years while interest is calculated half-yearly.
Answer:
Effective rate of interest = r = \(\left(1+\frac{0.14}{2}\right)^{2}\) – 1 = 15%
∴ C.I = A-P = 7500(1 + 0.15)4 – 7500 = ₹5617.5
Question 44.
Find the future value of an annuity of ₹ 5000 12% p.a for 6 years.
Answer:
Future value of an annuity = F = \(\frac{A\left((1+i)^{n}-1\right)}{i}\)
F = \(\frac{5000\left((1+0.12)^{6}-1\right)}{0.12}\) = ₹ 40,575.94
Question 45.
A radio is sold at a profit of 25% cost price and selling price are both increased by 100. If the new profit is at the rate of 20%, find the original cost of the radio, i.
Answer:
Let the original cost price be x
I: Profit = 25% SP = 1.25x
II: C.P. = 100 + x then SP= 1.25x + 100 ………(1)
Profit = 20%
S.P = (100 + x) + 0.2(100 + x) ……………..(2)
From 1 & 2 we get
1.25x + 100 = 100 + x + 20 + 0.2x
Solving we get x = ₹ 400 = original cost of the radio.
Question 46.
Prove that : \(\frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}\) = 1 + secA.cosecA
Answer:
\(\frac{\tan A}{1-\cot A}+\frac{\cot A}{1-\tan A}=\frac{\tan A}{1-\frac{1}{\tan A}}+\frac{\frac{1}{\tan A}}{1-\tan A}\)

= RHS
![]()
Question 47.
Find the area of a quadrilateral whose vertices are (1,2), (6,2), (5,3), and (3,4) taken in as order.
Answer:
Area of a quadrilateral = Area of ∆ABC + Area of ∆ACD
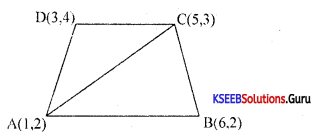
Area of ∆ABC = \(\frac{1}{2}\)Σx1 (y2 – y3) = \(\frac{5}{2}\) sq. units
Area of ∆ACD = 3 units
∴ Area of ∆BCD = \(\frac{5}{2}\) + 3 = \(\frac{11}{2}\)sq. units
Question 48.
Find the equation of a line through he intersection of the lines x – y + 2 = 0, 3x + 2y = 9 and parallel to the line 2x + y – 3.
Answer:
The point of intersection of the lines x -y + 2 = 0, 3x + 2y = 9 is (1, 3)
Any line parallel to the given line 2x + y = 3 is of the form 2x + y + k – 0
But this line passes through the point (1, 3)
2(1) + 3 + k = 0
∴ k = -5
Required equation of the line is 2x + y – 5 = 0
PART-E
V. Answer any ONE question: (6 × 5 = 30)
Question 49.
(a) Find the equation to the locus of a point moving in a plane such that it is equidistant from (-1, 1) and (4, 2). 4
Answer:
Let P(x, y) be the point on the locus
Given PA = PB where A = (-1, 1) B = (4, 2)
PA2 = PB2
(x + 1)2 + (y – 1)2 = (x – 4)2 + (y – 2)2
x2 + 2x +1 + y2 – 2y + 1 = x2 +16 – 8x + y2 + 4 – 4y
10x – 6y = 18 or 5x – 3y = 9 is the required equation of the locus.
(b) Solve for x if:
x = sec30°, tan60° + sin45°cosec45° + cos30°.cot60°.
x = \(\frac{2}{\sqrt{3}} \cdot \sqrt{3}+\frac{1}{\sqrt{2}} \sqrt{2}+\frac{\sqrt{3}}{2} \cdot \frac{1}{\sqrt{3}}\)
x = 2 + 1 + \(\frac{1}{2}\) = 3 + \(\frac{1}{2}\)
x = \(\frac{6+1}{2}=\frac{7}{2}\) ⇒ x = \(\frac{7}{2}\)
(c) Find the number of digits in the integral part of 320. (2M)
Answer:
Consider log320 = 20 log 3 = 20 × 0.4771 = 9.542
Since the characteristic is 9, there are 10 digits in 320.
![]()
Question 50.
(a) A firm finds that the production cost directly attributed to each product is 25 and fixed costs are 10,000. If each product can be sold for 35, find the
(i) cost function (ii) revenue function
(iii) profit function (iv) break-even level of output.
Answer:
V.C. = ₹ 125 , F.C. = ₹ 10,000, price = ₹ 35
(i) cost function = C(x) = 10,000 + 25x
(ii) Revenue function = R(x) = P × x = 35x
(iii) Profit function = TR – TC = 35x – 10,000 – 25 = 10x – 10,000.
At B.E. level of output T.R. = T.C.
35x = 10,000 + 25x
10x = 10,000
⇒ x = 10,000 units
(b) Find the sum to n terms of the series 5 + 55 + 555 + ……………………
Answer:
Let S = 5 + 55 + 555 +…………… to n terms
\(\frac{\mathrm{S}}{5}\) = 1+ 11 + 111+………..to n terms
\(\frac{9 \mathrm{~S}}{5}\) = 9 + 99 + 999 +…………… to n terms
=(10 – 1) + (100 – 1) + (1000 – 1) +……….. to n terms
= (10 + 100 + 1000 +………… to n terms) – (1 + 1 + 1………. to n ternis)
= \(\frac{10\left(10^{n}-1\right)}{9}\) – 1 × n
S = \(\frac{5}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)
(c) The HCF of two numbers is 16 and their LCM is 160. If each of the numbers is 64, then find the other number.
Answer:
Given H = 16, L = 160, a = 64, b = ?
H × L = a × b
b = \(\frac{H \times L}{a}=\frac{16 \times 160}{64}\) =40
∴ the other number is 40.