1st PUC Basic Maths Model Question Paper 7 with Answers

Students can Download 1st PUC Basic Maths Model Question Paper 7 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Model Question Paper 7 with Answers

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any TEN questions. (10 × 1 = 10)

Question 1.
Write the canonical representation of 96.
Answer:

Question 2.
Define an equivalence relation.
Answer:
A relation R on a set A is called an equivalence relation if it is reflexive. symmetric and transitive.

Question 3.
Simplify: 5(5°) + (52)°
Answer:
5¹ + (25)° = 5 + 1 = 6.

Question 4.
Find ‘x’ if log 625 = 4.
Answer:
x⁴ = 625 ⇒ x⁴ = 5⁴ ⇒ x = 5.

Question 5.
Find the 30th term of the AP -2, -5, 8,………………..
Answer:
a = -2 d = 5 + 2 – 3
T₃₀ = a + (30 – 1)d
= -2 + (29)(-3) = -2 – 87 = -89.

Question 6.
Form the quadratic equation whose roots are 1, 2.
Answer:
(x – 1)(x – 2) = 0 ⇒ x² – 3x + 2 = 0.

Question 7.
Calculate the S.I. on Rs. 18,000 for 4 months at 12\(\frac{1}{2}\)% per annum.
Answer:
P= 18,000 T = \(\frac{4}{12}=\frac{1}{3}\)R = \(\frac{25}{2}\)%

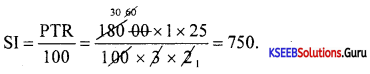
Question 8.
Write the formula to find the future value of Annuity Due.
Answer:
F = \(\frac{\mathrm{A}\left[(1+r)^{n}-1\right]}{r}\)(1 + r)

Question 9.
A person bought a cycle for Rs. 3000. For what price should he sell it to gain 10%?
Answer:
SP = \(\frac{100+\text { gain } \%}{100}\) × CP = \(\frac{100+10}{100}\) × 3000 = \(\frac{110}{100}\) × 3000 = Rs. 3300

Question 10.
Convert 15° into radian measure.
Answer:
15° = \(\frac{15 \pi}{180}=\frac{\pi^{c}}{12}\)

Question 11.
If A = 45°, then prove that sin 2A = 2 A. Cos A.
Answer:
Sin 2A = Sin 90° = 1
2 sin A cos A = 25 in 45° cos 450 = 2\(\frac{1}{\sqrt{2}} \frac{1}{\sqrt{2}}\) = 1
∴ LHS = RHS.

Question 12.
Find the equation to the locus of a point moving in a plane such that the sum of the squares of its distance from the coordinate axes is 2.
Answer:
x² + y² = 2.

PART -B

II. Answer any TEN questions. (10 × 1 = 10)

Question 13.
Find the imaginary part of (1 + i) (4 – 3i).
Answer:
(1 + i) (4 – 3i) = 4 – 3i + 4i + 3 = 7 + i
imaginary’ part = i.

Question 14.
Find the HCF \(\frac{8}{9}, \frac{32}{81}, \frac{16}{27}\)
Answer:
HCF of Numerators 8, 32, 16 = 8
LCM of Denominators 9, 81, 27 = 81
∴ HCF of fractions = \(\frac{\text { HCF of Numerators }}{\text { LCM of Denominators }}=\frac{8}{81}\)

Question 15.
If A = {3, 5, 7},B = {5, 7, 9} and U = {1, 2, 3, 4, 5, 6, 7, 8, 9} then find(A – B) × B’.
Answer:
A – B = {3}
B’ = {1, 2, 3, 4, 6, 7, 8)
(A – B) × B = {(3, 1), (3, 2), (3, 3), (3, 4), (3, 6), (3, 7), (3. 8)}.

Question 16.
If the 5th term of a HP is \(\frac{1}{5}\) and its 7th term is \(\frac{6}{5}\), find the 10th term.
Answer:
5th term of HP = \(\frac{1}{5}\)
5th term of AP = 5
a + 4d = 5 ………………..(1)
Seventh term of HP = \(\frac{6}{5}\)
Seventh term of AP = \(\frac{5}{6}\)
a + 6d = \(\frac{5}{6}\) ………….(2)

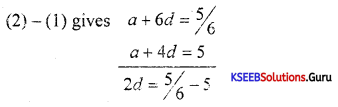
= –\(\frac{25}{6}\)
d = –\(\frac{25}{12}\)

a + 4d = 5 ⇒ a + 4\(\left(-\frac{25}{12}\right)\) = 5 ⇒ a – \(\frac{25}{3}\) = 5
a = 5 + \(\frac{25}{3}=\frac{15+25}{3}=\frac{40}{3}\)
Tenth term of AP = a + 9d
= \(\frac{40}{3}+9\left(\frac{-25}{12}\right)=\frac{40}{3}+\frac{3(-25)}{4}=\frac{160-225}{12}=\frac{-65}{12}\)
Tenth term of the corresponding HP = –\(\frac{-12}{65}\) .

Question 17.
Nine tables and eight chairs cost Rs. 456. Eight tables and nine chairs cost Rs. 462. Find the cost of each chair and each table.
Answer:

9x + 8 (30) = 456
9x + 240 = 456
9x = 456 – 240
9x = 216
x = 24.
∴ Cost of 1 table = Rs. 24
Cost of 1 chair = Rs. 30.

Question 18.
Solve: \(\frac{x-5}{10}+\frac{x+5}{5}\) = 5
Answer:
\(\frac{x-5}{10}+\frac{x+5}{5}\) = 5
x – 5 + 2x + 10 = 50
3x + 5 = 50
3x + 45
x= 15

Question 19.
Solve the following system of linear inequalities. 2 (x – 1) < x + 5 and 3 (x + 2) > 2 – x.
Answer:
2x – 2 < x + 5 and
2x – x < 5 + 2
x < 7……………(1)

3 (x + 2) > 2 – x
4x > 2 – 6
4x > – 4
x > \(\frac{-4}{45}\)
∴ x > -1 ……………(2)
From (1) and (2)
-1 < x < 7.

Question 20.
The average age of Ashok and Abdul is 45 years, the average age of Abdul and Anthony is 50years and the average age of Anthony and Ashok is 35 years. Find the ages of Ashok and Anthony.
Answer:
Age of Ashok = x
Age of Abdul =y
Age of Anthony = z
Given,
\(\frac{x+y}{2}\) = 45 ⇒ x + y = 90 ………………….(1)
\(\frac{y+z}{2}\) = 50 ⇒ y + z = 100 …………………(2)
\(\frac{z+x}{2}\) = 35 ⇒ z + x = 70 2 ………………….(3)

Add (1), (2), (3)
2x + 2y + 2z = 260
x + y – z = 130
x+ 100 = 130
x = 30

x + y = 90
30 + y = 90
y = 60
z = 100

60 + z = 100
z = 40

Age of Ashok = 30 years.
Age of Abdul = 60 years.
Age of Anthony = 40 years.

Question 21.
Prove that cos 189° + cos 9° = 0.
Answer:
Cos (180 + 9) + cos 9 = – cos 9 + cos 9 = 0.

Question 22.
Three consecutive vertices of a parallelogram are (3, 0), (5, 2) and (-2, 6). Find the fourth vertex.
Answer:
A = (3, 0) B = (5, 2) C = (-2, 6) D = (x, y)
Mid point of AC = mid point of BD
\(\)
3 – 2 = 5 + x
1 = 5 + x
x = -4

0 + 6 = 2 + y
y = 4
D = (- 4, 4).

Question 23.
Find the equation to the locus of a point moving in a plane that is equidistant from (- 1, – 1) and (4, 2).
Answer:
Let P(x, y) be a point which is equidistant from A (-1, -1) and B (4, 2)
Then |PA| = |PB|
Squaring PA2 = PB2
(x + 1)² + (y + 1)² = (x – 4)² + (y – 2)²
i,e. x² + 2x + 1 + y² + 2y + 1 = x² – 8x + 16 + y² – 4y + 4
i.e. 2x + 2y + 2 = – 8x- 4y + 20
i.e. 5x + 3y = 9
Hence the locus of P is the straight-line 5x + 3y = 9.

Question 24.
Find the equation of a line perpendicular to 3x – 2y + 1 = 0 and passing through the point ( 1, -2).
Answer:
Slope of the given line 3x – 2y + 1 = 0 is \(\frac{3}{2}\) = m₁
Since the two lines are perpendicular m₁ m₂ = – 1
m₂ = \(\frac{-1}{m_{1}}=\frac{-1}{3 / 2}=\frac{-2}{3}\)
Thus the equation of the line with slope m = \(\frac{-2}{3}\) and passing through
(x₁, y₁) = (1, -2) is given by
y – y₁ = m(x – x₁)
y + 2 = \(\frac{-2}{3}\)(x – 1)
⇒ 3y + 6 = -2x + 2
⇒ 2x + 3y + 4 = 0.

Question 25.
If the lines x – 2y + 1 = 0, 2x – 5y + 3 = 0 and 5x – 9y + k = 0 are concurrent, find k.
Answer:

y = 1
2x – 4 + 2 = 0 ⇒ 2x – 2 = 0 ⇒ x = 1 ,
5 (1) – 9 (1) + k= 0
– 4 + k = 0
k = 4
Point of concurrency = (1, 1).

PART-C

III. Answer any TEN questions: (10 × 3 = 20)

Question 26.
Three bells toll at intervals of 30 seconds, 40 seconds, and 50 seconds respectively. They start together. After how many minutes will the next bell toll together?
Answer:
Find the LCM of 30, 40 and 50

LCM = 30 × 20 = 600
Hence the bells will fall together after 600 sec.
Or \(\frac{600}{60}\) = 10 minutes.

Question 27.
If f(x) = x and g (x) = x³ + 1, find fog (1), gof (1) and fof (2) .
Answer:
(fog)(1) = f[g(1)] = f[2] = 2
(gof)(1) = g[f(1)] = g[1] = 1 + 1 = 2
(fof)(2) = f[f(2)] = f(2) = 2.

Question 28.
If 2^1/a = 3^1/b = 54^1/c show that a + 3b = c.
Answer:
∴ 2^1/a = k ⇒ 2 = k^a
3^1/b = k ⇒ 3 = k^b
54^1/c = k ⇒ 54 = k^c
Now 2 × 3³ = 54
k^a.(k^b)³ = k^c ⇒ k^ak^3b = k^c
∴ k^a+3b = k^c ⇒ a + 3b = c.

Question 29.
Prove : log_y x². log_z y³. log_x z⁵ = 30.
Answer:
LHS = 2 log_y x. 3log_z y. 5log_x z

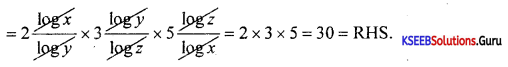
Question 30.
30. Find three numbers in GP. whose sum is 39 and their product is 729.
Let the three numbers be \(\frac{a}{r}\), a, ar
Product = 729
⇒ a³ = 729 ⇒ a³ = 91 ⇒ a = 9
Sum = 39
\(\frac{a}{r}\) + a + ar = 39
\(\frac{a}{r}\) + 9 + 9r = 39
\(\frac{a}{r}\) + 9r = 39 – 9
\(\frac{a}{r}\) + 9r = 30 ⇒ 9 + 9r² = 30r ⇒ 9r² – 30r + 9 = 0
⇒ 9r² – 27r – 3r + 9 = 0
9r(r – 3) – 3(r – 3) = 0
(r – 3)(9r – 3) = 0
r = 3 or 9r = 3
r = 3 or r = \(\frac{3}{9}=\frac{1}{3}\)
r = 3 or r = \(\frac{1}{3}\)

The numbers are \(\frac{a}{r}\),a,ar
\(\frac{9}{3}\), 9, 9(3)
3, 9, 27.

Question 31.
If α and β are the roots of the equation 2x – 5x + 7 = 0, then evaluate \(\frac{\alpha^{2}}{\beta}+\frac{\beta^{2}}{\alpha}\)
Answer:
\(\frac{\alpha^{2}}{\beta}+\frac{\beta^{2}}{a}=\frac{\alpha^{3}+\beta^{3}}{a \beta}\)

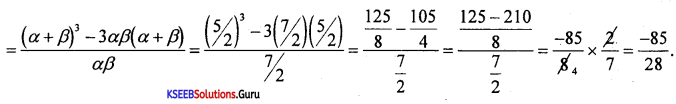
Question 32.
Rs. 16,000 invested at 10% p.a. interest compounded semiannually amounts to Rs. 18,522. Find the period of investment.
Answer:
P = Rs. 16,000
A = Rs. 18,522
R = 10%
q = 2
r = \(\left(1+\frac{\mathrm{R}}{q}\right)^{q}\) – 1 = \(\left(1+\frac{0.10}{2}\right)^{2}\) – 1 = (1 + 0.05)² – 1 = (1.05)² – 1 = 1.1025 – 1
= 0.1025 = 10.25%
A = P (1 + r)ⁿ
18522 = 16000(1 + 0.1025)ⁿ
\(\frac{18522}{16000}\) = (1.10025)ⁿ
1.157625 = (1.1025)ⁿ
log (1.157625) = n log 1.1025
n = \(\frac{\log (1.157625)}{\log 1.1025}=\frac{0.0635}{0.0423}\) = 1.501 ≈ 1.5
∴ n = 1.5 years.

Question 33.
The rate of a movie ticket was Rs. 150. This was reduced by 20%, due to which the revenue increased by 20%.
What was the percentage increase in the number of viewers?
Answer:
Let the no. of initial viewers be 100 Cost of each ticket = Rs. 150
Revenue generated initially = 150 × 100 = Rs. 15000
After the reduction in price cost of each ticket
= 150 – 20% of 150 = 150 – \(\frac{20}{100}\) × 150 = 150 – 30 = Rs.120
New revenue generated = 15000 + 20% of 15000 20
= 15000 + \(\frac{20}{100}\) × 15000 = 15000 + 3000 = Rs. 18000 100
No. of viewers = \(\frac{\text { Total revenue }}{\text { Cost of each ticket }}=\frac{18000}{120}\) = 150
Percentage increase in the no. of viewers = 150 – 100 = 50%.

Question 34.
For the first year of production, the fixed cost for setting up a new company is Rs. 3,00,000 and the variable cost is 70. The company expects revenue from sales to be Rs. 270 per unit of the product. Find the revenue function, cost function, and the break-even output.
(i) Construct the revenue function.
(ii) Construct the cost function.
(iii) Find the Break-Even output
(iv) Find the number of Calculator produced for which the company will suffere loss.
Answer:
C (x) = 70x + 3,00,000,
R(x)=270x
P(x) = R(x) – C(x)
270 x = (70x + 3,00,000) = 200x – 3,00,000

For BEP P(x)= 0
R(x) = C(x)
270x = 70x + 3,00,000, 20x = 3,00,000
x = 1500 BEP
less than x = 1500 units the company will suffer loss.

Question 35.
The angles of a triangle are in the ratio 2: 3: 5. Find them in degrees and radians.
Answer:
2 : 3 : 5 or 2x, 3x, 5x.
2x + 3x + 5x – 180
10x = 180 ⇒ x – 18°
2x = 2 (18) = 36° 36 × \(\frac{\pi}{180}=\frac{\pi^{c}}{5}\)
3x = 3 (18) = 54°
= \(\frac{54 \pi}{180}=\frac{3 \pi}{10}\)
5x = 5(18) = 90° = \(\frac{\pi}{2}\).

Question 36.
Find ‘x’ given : \(\frac{x \cdot \sin ^{2} 300^{\circ} \sec ^{2} 240^{\circ}}{\cos ^{2} 225^{\circ} \cdot \cos e c^{2} 240^{\circ}}\) = cot 315.tan2 300°.
Answer:
sin300 = sin(360 – 60) = -sin60 = \(\frac{-\sqrt{3}}{2}\)
sec 240 = sec (180 + 60) = – sec 60° = – 2
cos225 = cos(180 + 45°) = -cos45° = –\(\frac{1}{\sqrt{2}}\)
cosec 240 = cosec (180 + 600) = cosec 60 = –\(\frac{2}{\sqrt{3}}\)
cot 315° = cot(360 – 45°) – cot45° = -1
tan 300 = tan (360 – 600) = – tan 600 = –\(\sqrt{3}\)
∴ The given equation becomes:
\(\frac{x \cdot \frac{3}{4} \cdot 4}{\frac{1}{2} \cdot \frac{4}{3}}\) = 1.3
⇒ x = \(\frac{6}{9}=\frac{2}{3}\)

Question 37.
Show that the points A(2, 4), B(2, 6) and C(2 + \(\sqrt{3}\), 5) form the vertices of an equilateral triangle.
Answer:
AB = \(\sqrt{(2-2)^{2}+(6-4)^{2}}=\sqrt{0+4}=\sqrt{4}\) = 2
BC = \(\sqrt{(2+\sqrt{3}-2)^{2}+(5-6)^{2}}=\sqrt{3+1}=\sqrt{4}\) = 2
CA = \(\sqrt{(2+\sqrt{3}-2)^{2}+(5-4)^{2}}=\sqrt{3+1}=\sqrt{4}\) = 2
AB = BC = CA
∴ A, B, C form an equilateral triangle.

Question 38.
Derive the equation of a straight line in slope-intercept form.
Answer:

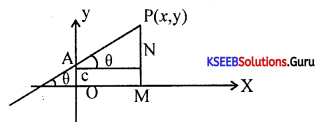
Slope of AP = m = tan θ = \(\frac{P N}{\mathrm{AN}}=\frac{P M-M N}{O M}\)
\(\frac{\mathrm{PM}-\mathrm{OA}}{\mathrm{OM}}=\frac{\mathrm{Y}-\mathrm{C}}{x}\)
∴ y – c = mx ⇒ y = mx + c.

PART -D
III. Answer any SIX questions. (6 × 5 = 30)

Question 39.
In a certain college with 500 students, 300 take the milk and 251 take tea. Assuming that every student takes at least one of the two, find how many take.
(a) both milk and tea
(b) milk only
(c) tea only
Answer:
n (M ∪ T) = 500
n (M) = 300
n (T) = 250
n (M ∪ T) = n (M) + n (T) – n (M ∩ T)
n (M ∩ T) = n (M) + n (T) – n (M ∪ T) = 300 + 250 – 500
n (M ∩ T) = 50
n (M – T) = n (M) – n (M ∩ T) = 300 – 50 = 250
n(T – M) = n(T) – n(M ∩ T) = 250 – 50 = 200.

Question 40.
Evaluate using log tables: \(\frac{25.36 \times 0.4569}{847.5}\)
Answer:
Let x = \(\frac{25.36 \times 0.4569}{847.5}\)
log x = log 25.36 + log 0.4569 – log 847.5
= 1.4041 + 1.6599 – 2.9282
= 1.4041 – 1 + 0.6599 – 2.9282
= – 1.8642
= – 1 – 0.8642 = – 1 + 1 -0. 8642
= -2 + 0.1358
= 2.1358
= 01368

Question 41.
Find the sum to ‘n’ terms of the series 4 + 44 + 444 +……………..
Answer:
S_n = 4 + 44 + 444 + …………………….. to n terms
S_n = 4(1 + 11 + 111 + …………………….. to n terms)
\(\frac{9 \mathrm{~S}_{n}}{4}\) = 9 + 99 + 999 + ……………. to n terms
\(\frac{9 \mathrm{~S}_{n}}{4}\) = (10 – 1) + (10² – 1) + (10³ – 1) +……………………
= (10 + 10² + 10³ + ………………. ) – (1 + 1 + 1 +………………… )
\(\frac{9 S_{n}}{4}=\frac{10\left(10^{n}-1\right)}{10-1}\) – n
S_n = \(\frac{4}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]\)

Question 42.
Solve the cubic equation x³ + 6x² + 9x + 4 = 0 using synthetic division, given that there is an integral root between – 3 and 3.
(1) x³ + 6x² + 9x + 4 = 0
Answer:
Put x = – 1
(-1)³ + 6(-1)² + 9 (-1) + 4
= -1 + 6 – 9 + 4
= 10 – 10 = 0
∴ x = – 1 is a root of the equation
∴ x + 1 is the factor (factor theorem)

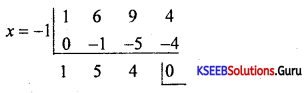
Quotient = x² + 5x + 4
remainder = 0
x³ + 6x² + 9x + 4 = 0.
(x + 1)(x² + 5x + 4) = 0
x + 1 = 0, x² + 5x + 4 = 0
x² + 4x + x + 4 = 0
x(x + 4) + 1 (x + 4) = 0
(x + 4)(x + 1) = 0
x = -4, x = -1
The roots are -1, -1, -4.

Question 43.
If the difference between simple interest and compound interest for 3 years at 2.5% p.a. is Rs. 625, find the sum invested.
Answer:
Let the sum invested = P
r = 2.5% p.a. = 0.025 p.a.
n = 3 years
A = P(1 +r)ⁿ = P(1 +0.025)³ = P (1.025)³
CI = A – P = P (1.025)³ – P = P [(1.025)3 – 1] = P (0.07689)
SI
r = 2.5
T = 3
SI = \(\frac{P \times T \times R}{100}=\frac{P \times 3 \times 2.5}{100}\) = 0.075P
∴ CI – SI = 625
0.07689P – 0.075 P = 625
∴ 0.00189 P = 625
P = 3,30687.83
∴ P = Rs. 3,30,687.83.

Question 44.
How much should you invest if you want to receive Rs.5000 at the beginning of each year for the next 5 years and the Cl is 16% p.a. compounded quarterly.
Answer:
A = Rs. 5,000 n = 5 years R = 0.16 q = 4
r = \(\left(1+\frac{\mathrm{R}}{q}\right)^{q}\) – 1 = \(\left(1+\frac{0.16}{4}\right)^{4}\) – 1 = 0.1698 = 16.98
Effective rate of interest = 16.98%
P = \(\frac{A\left[(1+r)^{n}-1\right]}{r(1+r)^{n}}\)(1 + r)
= \(\frac{5000\left[(1+0.1698)^{5}-1\right]}{0: 1698(1.1698)^{5}}\)(1.1698) = \(\frac{6963}{0.3719}\) = 18,722.77

Question 45.
Ram Singh purchased 2 camels for Rs. 18,000 and Rs. 15,000 respectively. He sold them at a loss of 15% and a gain of 19% respectively. Find the selling price of each camel. Also, find the overall loss or gain percent in this transaction.
Answer:
C.P of camel = 18000
S.P while sold at loss of 15% = \(\frac{85}{100}\) × 18000 = 15300
C.P. of second camel = 15000
S.P. while sold at gain of 19% = \(\frac{119}{100}\) × 15000 = 17,850
Total CP = 18000 + 15000 = 33000
Total S.P. = 15,300 + 17,850 = 33150
∴ Profit = 33,150 – 33000 = 150
Profit % = \(\frac{150}{33000}\) × 100 = 0.45%.

Question 46.
Prove: \(\frac{\tan \theta}{\sec \theta-1}+\frac{\tan \theta}{\sec \theta+1}\) = 2 cosec θ
Answer:

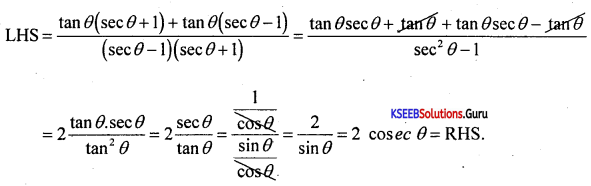
Question 47.
Find the area of the quadrilateral whose vertices are A (1, 2), B (6, 2), C (5, 3) and D (3,4).
Answer:
(1,2) (6,2) (5, 3) (3,4)
∆ ABC = 1/2 [1 (2 – 3) + 6(3 – 2) + 5 (2 – 2)]
= 1/2 [1 (-1) + 6 (1) + 5 (0)] = 1/2 [-1+6 + 0] = \(\frac{5}{2}\)
ACD = 1/2 [1 (3 – 4) + 5 (4 – 2) + 3 (2 – 3)]
= 1/2 [1 (-1) + 5 (2) + 3 (-1 )] = 1/2 [-1 + 10 – 3] = 1/2 [10-4 ] = 1/2 (6) = 3
Area of the quadrilateral ABCD
= |Area of ∆ABC| + | Area of ∆ACD| = \(\left|\frac{5}{2}\right|\) + |3| = \(\frac{5}{2}\) + 3 = \(\frac{5+6}{2}\) = \(\frac{11}{2}\)sq. unit.

Question 48.
Find the equations of lines passing through the point (3, 4) and having intercepts on the axes such that their sum is 14.
Answer:
Let the x and y intercepts of the line be a and b respectively so that a + b = 14 or b = 14 – a
Thus the equation of the line in the intercept form is
\(\frac{x}{a}+\frac{y}{14-a}\) = 1
But it passes through the point(3,4).
therefore \(\frac{3}{a}+\frac{4}{14-a}\) – 1
3 (14 – a) + 4a = a (14 – a)
i.e., a² – 13a + 42 = 0
i.e., (a – 6) (a – 7) = 0
or a = 6 or a = 7
If a = 6 then b = 8; If a = 7 then 6 = 7

Therefore equations of the lines are \(\frac{x}{6}+\frac{y}{8}\) = 1 or \(\frac{x}{7}+\frac{y}{7}\) = 1
i.e., 4x + 3y – 24 = 0 or x + y – 7 = 0.

PART-E

III. Answer any ONE question. (1 × 1 = 10)

Question 49.
(a) If A {1, 2, 3, 4}, B = {3, 4, 5, 6}, C = {4, 5, 6, 7, 8}, then verify:
(i) A ∪ (B ∩ C) = ( A ∪ B) ∩ ( A ∪ C)
(ii) A∩(B∪C) = (A∩B)∪(A∩C)
Answer:
(i)Let A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
C = {4, 5, 6, 7, 8}
B∩C = {4,5,6}

A∪(B∩C) = {1, 2, 3, 4} ∪ {4, 5, 6}
= {1,2, 3, 4, 5, 6}

A∪B = {1, 2, 3, 4, 5, 6}
A∪C = {1, 2, 3, 4, 5, 6, 7, 8}
(A∪B) ∩ (A∪C)
= {1, 2, 3, 4, 5,6} ∩ {1, 2, 3,4, 5, 6, 7, 8}
= {1, 2, 3, 4, 5, 6}
A∪(B∩C) = (A∪B) ∩ (A∪C)

(ii) B∪C = {3, 4, 5, 6, 7, 8}
A∩(B∪C)= {1, 2, 3, 4} ∩ {3, 4, 5, 6, 7, 8}
= {3, 4}
A∩B = {3, 4}
A∩C = {4}
(A∩B)∪(A∩C) = {3, 4}
Thus we have
A∩(B∪C) = (A∩B) ∪ (A∩C).

(b) Find the future value of an annuity of Rs. 5000 at 12% p.a. for 6 years.
Answer:
A = Rs. 5,000 r = 0.12 n = 6
F = \(\frac{\mathrm{A}\left[(1+r)^{n}\right]}{r}=\frac{5000\left[(1+0.12)^{6}-1\right]}{0.12}=\frac{4869.11}{0.12}\) =40,575.9

(c) The average age of 12 boys is 8 years. Another boy of 21 years joins the group. Find the average age of the new group.
Answer:
Average age of 12 boys = 8 years
∴ Total age of boys = 8 × 12 = 96 years
when a boy of 21 yrs joins the group,
the total age of 13 boys = 96 + 21 = 117 years
∴ Average age of the new group = \(\frac{117}{13}\) = 9 years.

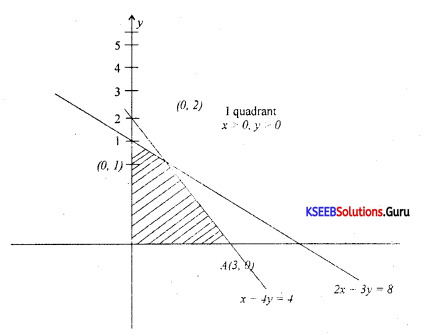
50. (a) Solve the linear inequalities graphically :
3x + 3y ≤ 6,
x + 4y ≤ 4,
x ≥ 0,y ≥ 0.
Answer:

(b) A watch manufacturer finds that his total cost function is linear. The total cost for 100 watches is Rs. 20,000 and for 200 watches, the total cost increased to Rs. 30,000. What are the fixed cost and variable cost per unit?
Answer:
Total cost = T.V.C. + T.F.C.
C (x) = ax + b
When x = 100 watches
T.C. = a (100) + b
i.e.20,000 = 100a+ 6 …………………. (1)

Similarly when x = 200 watches
30.0 = 200 a + b ……………….(2)
(2) – (1)30,000 = 200 a + b
-20,000 = 100 a + b
10,000 = 100 a
a = \(\frac{10,000}{100}\) = 100 substitute in (1)
20,000= 100 (100) + b
20,000 = 10,000 + b
b =10,000

∴ When x = 150, TC = (100) (150)+ 10,000
= 15,000+10,000,
TC = ₹ 25,000.

(c) The HCF of 2 numbers is 16 and their LCM is 160. If one of the numbers is 32, then find the other num ber.
Answer:
HCF =16 LCM =160 a = 32 b = ?
a × b = H × L
b = \(\frac{\mathrm{H} \times \mathrm{L}}{a}=\frac{16 \times 160}{32}=\frac{2560}{32}\) = 80
∴ The other number is 80.