Students can Download 1st PUC Basic Maths Model Question Paper 6 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Model Question Paper 6 with Answers
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any ten questions (10 × 1 = 10)
Question 1.
Find the imaginary part of 1 + i
Answer:
1 + \(\frac{1}{i}\) = 1 + \(\frac{1}{i}\) × \(\frac{i}{i}\) = 1 + \(\frac{i}{i^{2}}\) = 1 + \(\frac{i}{-1}\) = 1 – i
∴ Imaginary part = -1
Question 2.
If A = {5, 6}, B = {7, 8} find B × A
Answer:
B × A = {(7, 5), (7, 6), (8, 5), (8, 6)}
Question 3.
If f: R → R is defined byf(x) = 5x + 3 then find f(1/5)
Answer:
f(1/5) = 5(1/5) + 3 = 1 + 3 = 4
Question 4.
If log2 \(\sqrt{32}\) = x then solve for x.
Answer:
log2 \(\sqrt{32}\) = x ⇒ \(\sqrt{32}\) = 2x ⇒ (25)1/2 = 2x ⇒ 25/2 = 2x ⇒ x = \(\frac{5}{2}\)
Question 5.
Simplify \(\left(\frac{9}{4}\right)^{-3 / 2}\)
Answer:
\(\left(\frac{9}{4}\right)^{-3 / 2}=\left(\frac{4}{9}\right)^{3 / 2}=\left[\left(\frac{2}{3}\right)^{2}\right]^{3 / 2}=\left(\frac{2}{3}\right)^{3}=\frac{8}{27}\)
Question 6.
Find the 12th term of the A.P 1, 4, 7, ………..
Answer:
a = 1, d – 3, T12 = ?, n = 12
Tn = a + (n – 1)d
T12 = 1 + (12 – 1)(3) = 1 + 11(3) = 1 + 33 = 34
![]()
Question 7.
Solve for x. 3(x + 5) – 25 = 9 + 2(x – 7)
Answer:
3 (x + 5) – 25 = 9 + 2 (x – 7)
3x + 15 – 25 = 9 + 2x – 14
3x- 10 = 2x- 5
3x- 2x = 10 + 5
x = 5
Question 8.
Convert \(\frac{4}{5}\) into percentage
Answer:
\(\frac{4}{5}=\frac{4}{5}\) × 100% = 4 × 20 = 80%
Question 9.
Convert 300° into radians.
Answer:
300° = 300 × \(\frac{\pi}{180}=\frac{5 \pi^{C}}{3}\)
Question 10.
If the slope of the line AB is \(\frac{5}{2}\) and AB is perpendicular to- CD then find the slope of CD.
Answer:
Slope of = \(\frac{-2}{5}\)
Question 11.
Find the simple interest on Rs. 1500 at 4% p.a. for 145 days.
Answer:
P = 1500 t = \(\frac{145}{365}\) R = 4%
SI = \(\frac{\mathrm{PTR}}{100}=\frac{1500 \times \frac{145}{365} \times 4}{100}\) =23.83523.84
Question 12.
Write the formula for the present value of an annuity due.
Answer:
P = \(\frac{\mathrm{A}\left[(1+r)^{n}-1\right]}{r(1+r)^{n}}\)(1 + r)
PART-B
II. Answer any Ten questions. (10 × 2 = 20)
Question 13.
Find the H.C.F of 55 and 210.
Answer:

The last non-zero remainder is 5, (55, 210) = 5
Question 14.
U = {1,2,3,4, 5,6, 8,9}, A = {1,2,3,4, 5}, B = {3, 4,5, 6, 7} Prove that (A∪B)’ = A’∩B’.
Answer:
A∪B ={1,2,3,4,5,6,7}
(A∪B)’ = {8,9} …………….(1)
A’ = {6, 8, 9}
B’ ={1,2, 8, 9}
A’∩ B’ = {8, 9} ……………..(2)
From (1) and (2) (A∪B)’ = A’∩B’
Question 15.
Prove that \(\frac{1}{1+x^{p-q}}+\frac{1}{1+x^{q-p}}\)
Answer:
LHS = \(\frac{1}{1+\frac{x^{p}}{x^{q}}}+\frac{1}{1+\frac{x^{q}}{x^{p}}}=\frac{x^{q}}{x^{q}+x^{p}}+\frac{x^{p}}{x^{p}+x^{9}}=\frac{x^{p}+x^{q}}{x^{p}+x^{q}}\) = 1 = RHS
![]()
Question 16.
Prove that loga \(\) = loga m – loga n.
Answer:
Let loga m = x ⇔ ax = m
loga n = y ⇔ ay = n
loga \(\left(\frac{\mathrm{m}}{\mathrm{n}}\right)\) = z ⇔ az = \(\frac{m}{n}\)
Consider az = \(\frac{\mathrm{m}}{\mathrm{n}}=\frac{\mathrm{a}^{x}}{\mathrm{a}^{\mathrm{y}}}\) = ax-y
= loga\(\left(\frac{\mathrm{m}}{\mathrm{n}}\right)\) = logam – logan
Question 17.
Insert 3 means between \(\frac{1}{4}\) and \(\frac{1}{64}\)
Answer:
Let g1, g2, g3 be the 3 GM’s between \(\frac{1}{4}\) and \(\frac{1}{64}\)
∴ \(\frac{1}{4}\) g1, g2, g3 \(\frac{1}{64}\) are in GP.
Here T5 = \(\frac{1}{64}\)
⇒ ar4 = \(\frac{1}{64}\)
\(\frac{1}{4}\) r4 = \(\frac{1}{64}\)
r4 = \(\frac{4}{64}=\frac{1}{16}=\left(\frac{1}{2}\right)^{4}\)
∴ r = \(\frac{1}{2}\)
∴ The 3 GM’s are \(\frac{1}{8}, \frac{1}{16}, \frac{1}{32}\)
Question 18.
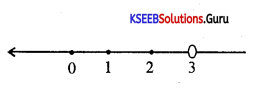
Solve 3x – 2 < 2x + 1, x ∈ R, represent the solution on the number line.
Answer:
3x – 2 < 2x + 1
3x – 2x < 2 + 1
x < 3
![]()
Question 19.
Find the quotient and remainder when 4x3 + 3x2 – 2x 1 is divided by x +1 using synthetic division.
Answer:
Here the multiplier is -1
x = -1
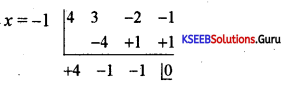
Quotient = 4x2 – x – 1 = 0 and Remainder = 0.
Question 20.
By selling 8 erasers a trader gains the selling price of 1 eraser, percent.
Answer:
Let the selling Price of one eraser be x then SP of 8 erasers = 8x
Profit =x
C.P =S.P- Profit
= 8x – x = 7x
Profit% = \(\frac{\text { Profit }}{\text { C.P }}\) × 100
= \(\frac{x}{7 x}\) × 100 = 14\(\frac{2}{7}\)%
Question 21.
Find the effective rate of interest when a sum lent at 18% p.a. is compounded quarterly.
Answer:
i = 0.18 q = 4
r = \(\left(1+\frac{i}{q}\right)^{q}\) – 1
= \(\left(1+\frac{0.18}{4}\right)^{4}\) – 1 = 0.1925
∴ r = 19.25%
Question 22.
The average weight of 10 boys is 30 kg. If an 11th boy is added then the average weight is r increased by 2 kg. Find the weight of the 11th boy.
Answer:
Total weight of 10 boys = 30 × 10 = 300 Kg.
Total weight of (10 + 1) boys = (30 + 2) 11
= 32 × 11
= 352 Kgs.
The weight of 11th boy added = (352 – 300) kg.
= 52 Kgs.
Question 23.
P.T. (1 + cot A – cosec A) (1 + tanA + sec.A) = 2
Answer:
L.H.S. = (1 + cot A – cosec A) (1 + tanA + sec.A)
= \(\left(1+\frac{\cos A}{\sin A}-\frac{1}{\sin A}\right)\left(1+\frac{\sin A}{\cos A}+\frac{1}{\cos A}\right)\)
= \(\left(\frac{\sin A+\cos A-1}{\sin A}\right)\left(\frac{\cos A+\sin A+1}{\cos A}\right)\)
= \(\frac{(\cos A+\sin A)^{2}-1}{\sin A \cos A}\)
= \(\frac{\cos ^{2} A+\sin ^{2} A+2 \cos A \sin A-1}{\sin A \cdot \cos A}\)
= \(\frac{1+2 \cos A \cdot \sin A-1}{\sin A \cdot \cos A}\)
= \(\frac{2 \cos A \cdot \sin A}{\sin A \cdot \cos A}\) = 2 = R.H.S
![]()
Question 24.
Show that points A(7, 9), B(3, -7), C(-3, 3) are the vertices of the right-angled isosceles triangle.
Answer:
AB2 = (7 – 3)2 + (9 + 7)2 = 272
BC2 = (-3 -3)2 + (3 + 7)2 =136
AC2 = (-7 -3)2 + (9-3 )2 = 136
Clearly AB2 = AC2 + BC2. Thus ABC is a right-angled triangle. Also, BC2 =AC2 which implies the BC = AC and so ABC is an isosceles triangle. Hence the given three points form a right-angled isosceles triangle.
Question 25.
Find the equation to the straight-line cutting of equal intercepts and passing through (-2,5)
Answer:
Let the straight line AB cut off equal Mercept with both the axes.
Let OA = OB = a
Hence equation of AB is given by \(\frac{x}{a}+\frac{y}{a}\) = 1
i.e. x + y = a
Since this line passes through (-2, 5) we get -2 + 5 = a i.e. a = 3
Hence the required equation of AB is x + y = 3
PART-C
III. Answer any ten questions. (10 × 3 = 30)
Question 26.
Prove that 2 + 3\(\sqrt{5}\) is an irrational number.
Answer:
If possible, let 2 + 3\(\sqrt{5}\) is rational
∴ 2 + 3\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\), p, q ∈ z, q ≠ 0
3\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) – 2 = rational – rational = rational.
∴ \(\sqrt{5}\) is irrational
∴ 3\(\sqrt{5}\) is irrational
∴ irrational number = a rational number which is a contradiction.
∴ our assumption is wrong.
∴ 2+ 3\(\sqrt{5}\) is irrational.
Question 27.
Out of 50 people, 20 people drink tea, 10 take-ups both tea, and coffee. How many take one of the two drinks. Show the result by Venn diagram.
Answer:
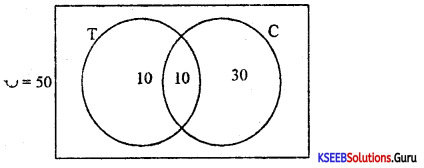
n (T ∪C) = n(T) + n(C) – n(T∩C)
50 = 20 + n (C) – 10
40 = n (C)
Number of people taking atleast one of the two drinks
10+ 10 + 30 = 40 + 10 = 50
Question 28.
Prove that \(\left(\frac{x^{2}}{x^{b}}\right)^{a^{2}+a b+b^{2}}\left(\frac{x^{b}}{x^{c}}\right)^{b^{1}+b c+e^{2}}\left(\frac{x^{e}}{x^{a}}\right)^{c^{2}+\infty+a^{2}}\) = 1
Answer:
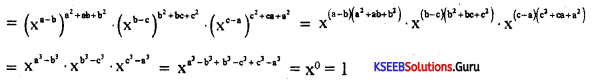
Question 29.
If log \(\left(\frac{\mathrm{a}-\mathbf{b}}{4}\right)\) = log\(\sqrt{a}\) + log\(\sqrt{b}\), Show that (a + b)2 = 20ab
Answer:
log\(\left(\frac{\mathrm{a}-\mathbf{b}}{4}\right)\) = lo\(\sqrt{a}\) + log\(\sqrt{b}\)
log\(\left(\frac{\mathrm{a}-\mathbf{b}}{4}\right)\) = log\(\sqrt{a b}\)
\(\frac{a-b}{4}\) = \(\sqrt{a b}\)
a – b = 4\(\sqrt{a b}\)
Squaring both sides, we get
(a-b)2 = 16 ab
a2 + b2 – 2ab = 16ab
a2 + b2 – 16ab = 2ab
a2 + b2 – 18ab
a2 + b2 + 2ab = 18 ab + 2ab
(a – b)2 = 20 ab
Question 30.
Ankur Choudhary agrees to pay the rent ₹ 30,000 for the first year ₹ 32,000 for the second year and so on each year the rent is increased by ₹ 2,000/- Find the total amount he paid for 10 years.
Answer:
a = 30,000
d = 2,000
n= 10
Now Sn = \(\frac{n}{2}\)[2a + (n- 1)d]
Sn = \(\frac{10}{2}\)(2(30,000) + (l0-l)2,000)
= 5[60,000 + 9(2,000)]
= 5(60,000 + 18,000]
= 5 [78,000]
= 3,90,000
∴ He paid 3,90,000 for 10 years.
![]()
Question 31.
Solve x3 – 2x2 – 5x + 6 = 0.
Answer:
Let f (x) = x2 – 2x2 – 5x + 6
f(1)= 1 – 2 – 5 + 6 = 7 – 7 = 0
∴ x = 1 is a root of the given equation. Let us remove this root by Synthetic division.
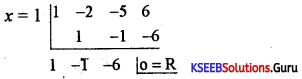
∴ The resulting equation is x2 – x – 6 = 0 is the quotient and remaind = 0
x2 – x – 6 = 0
(x – 3) (x + 2) = 0
x = 3 or -2
Thus x = 1, -2, 3 are the roots of the given equation.
Question 32.
₹ 9000 amounts to 10,418.652 in 3 years. Find the compound interest rate percent.
Answer:
P = 9000 A= 10,418.625 n = 3r = ?
i = Antilog\(\left[\frac{\log A-\log P}{n}\right]\) – 1
= Antilog\(\left[\frac{\log 10418.625-\log 9000}{3}\right]\) – 1
= Antilog\(\left[\frac{4.0174-3.9542}{3}\right]\) – 1
= Antilog[0.021067] – 1
= 1.050 – 1
= 0.05
R = i × 100
= 0.05 × 100 = 5%
Question 33.
A father wishes to divide 50,000 amongst his two daughters who are respectively 12 and 15 years old in such a way that the sum invested at 5% p.a compound interest will give the same amount to both of them when they attain the age of 18. How is the sum divided?
Answer:
Let the share of the older daughter = x then share of young one = 50,000 – x
For older daughter,
A = A1 P = x, i = 0.05, n = 3
A1 = x (1 + 0.05)3
For younger daughter
A1 = A2 P = 50,000 -x, i = 0.05 n = 6
Given A1 = A2
x(1.05)3 = (50,000 – x)(1.05)6
x = (50,000 – x)(1.05)3
x = 57881.25 = 1.157625 x
2.157625 x = 57881.25
x = 26826 (Approx.)
∴ Share of older daughter = ₹ 26826
Share of younger daughter = 50,000 – 26826 = ₹ 23174
Question 34.
A person repaid his loan in 10 equal annual installments starting from the beginning of the first year. If each installment was ₹ 6000 and compound interest charged was 12% p. a. What was the amount borrowed.
Answer:
a = 6000, n=10, i = 0.12. It is the present value of annuity due.
P = \(\frac{a\left[(1+i)^{n}-1\right]}{i(1+i)^{n}}\)(1 + i) = \(\frac{8000\left[(1+0.05)^{3}-1\right](1+0.05)}{(0.05)(1+0.05)^{3}}\)
= \(\frac{8000[(1 . .2763)-1](1.05)}{0.05 \times 1.2763}\) = ₹ 36369.50
![]()
Question 35.
The average age of 10 students in a class increases by 4.8 months. When a boy of age 6 years is replaced by a new boy. What is the age of the new boy?
Answer:
Let the average age of 10 boys = x years
Total age of 10 boys = 10x
After replacement of a boy of 6 years age and inclusion of new boys if his age is assumed to be y years.
Then the total age of 10 boys in a new group = (10x – 6) + y
Given the new average of 10 boys = (x + 4.8 months) or
= x + \(\frac{4.8}{12}\) years
= (x + 0.4) years
∴ Average of new group of 10 boys = \(\frac{\text { Total age of } 10 \text { boys }}{\text { No of boys }}\)
(x + 0.4) = \(\frac{(10 x-6)+y}{10}\)
10 (x + 0.4) = (10x – 6) + y
10x + 4 = 10x-6 + y
∴ y = 10
∴ Age of the new boy replaced = 10 years
Question 36.
P.T. (1 + sin θ + cosθ)2 = 2(1 + sinθ) (1 + cosθ)
Answer:
LHS. = {(1 + sin θ) + (cos θ)}2
= 1 + sin2θ + 2sinθ + cos2θ + 2cosθ (1 + sin θ)
= 2 + 2 sin θ + 2 cos θ (1 + sin θ)
= 2(1 + sin θ) + 2 cos θ (1 + sin θ)
= (1 + sin θ) (2 + 2 cos θ)
= 2 (1 + sin θ) (1 + cos θ)
Question 37.
Show that the points (1 -1) (5, 2) and (9, 5) are coolinear.
Answer:
We know that the three points A, B and C taken in this order are collinear if and only if AB + BC = AC
Let A= (1, -1), B = (5, 2) C = (9, 5)
Consider
AB = \(\sqrt{(5-1)^{2}+(2+1)^{2}}=\sqrt{16+9}\) = 5
BC = \(\sqrt{(9-5)^{2}+(5-2)^{2}}=\sqrt{16+9}\) = 15
AC = \(\sqrt{(-9-1)^{2}+(5+1)^{2}}=\sqrt{64+36}\) = 10
Clearly AB + BC = AC
⇒ The points, A, B and C are collinear
Question 38.
If the lines 2x – y = 5, Kx – y = 6 and 4x – y = 7 are concurrent, find K.
Answer:
We have 2x – y = 5 ….(1)
Kx – y = 5 ………(2)
4x – y = 7 ……..(3)
Solving (1) and (3) we get x = 1 and y = – 3
Since the lines are concurrent put x = 1 and y = 3 in (2)
We get K (1) – (-3) = 6 ⇒ K + 3 = 6 ⇒ K = 3
PART – D
IV. Answer any six questions. (6 × 5 = 30)
Question 39.
f(x) = x + 1 and g(x) = x2 + 1
Find (i) fog (1) (ii) fog (2) (iii) gof (1), (iv) gof (2) (v) fog (3)
Answer:
(i) fog(1) = f (g (1))
= f (2)
= 2 + 1 = 3
(ii) fog (2) = f(g(2))
= f(5)
= 5 + 1 = 6
(iii) gof (1) = gof(1)
= g(f(D)
= g (2) = 4 + 1 = 5
(iv) gof (2) = g(f(2))
= g (3)
= 9 + 1 = 10
(v) fog (3)
f(g(3))
f (10) = 10 + 1 = 11
Question 40.
Find the sum of 6 terms of the GP 1, 3, 9
Answer:
Here, a = 1, r = 3, n = 6
Sn = \(\frac{a\left(r^{n}-1\right)}{r-1}\)
Sn = \(\frac{729-1}{2}=\frac{729-1}{2}\) = 364
![]()
Question 41.
If \(\frac{2}{3}\), x, \(\frac{1}{x}\) areinH.Pfindx
Answer:
Given
\(\frac{2}{3}\), x, \(\frac{1}{2}\) are in H.P.
⇒ \(\frac{3}{2}\), \(\frac{1}{x}\), 2 are in A.P.
⇒ \(\frac{1}{x}-\frac{3}{2}\) = 2 – \(\frac{1}{x}\)
\(\frac{1}{x}+\frac{1}{x}=\frac{3}{2}\) + 2
\(\frac{2}{x}=\frac{7}{2}\)
\(\frac{x}{2}=\frac{2}{7}\)
∴ x = \(\frac{4}{7}\)
Question 42.
A certain two digits number is 2 times the sum of the digits, if 63 is added to the number the digits get interchanged. Find the number.
Answer:
Let the digit in ten’s place be x and digit in units place be v.
∴ The number is 10x + y
Given 10x + y = 2 (x + y)
8x – y = 0 ……………(1)
Also given 10x + y + 63 = 10y + x
9x – 9y + 63 = 0 ⇒ x – y + 7 = 0 ………….(2)
Solving (1) and (2), we get: x = 1 and y = 8
∴ The required number is 10x + y = 10
1 + 8 = 10 + 8 = 18.