Students can Download 1st PUC Basic Maths Model Question Paper 2 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.
Karnataka 1st PUC Basic Maths Model Question Paper 2 with Answers
Time: 3.15 Hours
Max. Marks: 100
Instructions:
- The questions paper consists of five parts A, B, C, D, and E.
- Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
- Write the question numbers properly as indicated in the questions paper
PART-A
I. Answer any ten questions (10 × 1 = 10)
Question 1.
Write the imaginary part of 4 – 5i
Answer:
-5
Question 2.
If A = {1, 2, 3, 4} and B = {1, 2, 3, 4, 5, 6, 7} find A – B.
Answer:
A – B = { }
Question 3.
If f: R → R is defined by f(x) = 3x + 5 then find f (-1)
Answer:
f(-1) = 3(- 1) + 5 = -3 + 5 = 2
Question 4.
Simplify (5°)2 + 5
Answer:
(1)2 + 5′ = 1 +5 = 6
Question 5.
Find the value of log10.01
Answer:
log100.01 = x ⇒ 10x = 0.01
10x = \(\frac{1}{100}\) ⇒ 10x = 10-2
x = -2
![]()
Question 6.
Find the 8th term of the progression -2, -4, -6……….
Answer:
a = -2, d = -4 + 2 = -2, n = 8, T8 = ?
Tn = a + (n – l)d, T8 = -2 + (8 – 1) (-2) = -2 + 7(-2) = -2 – 14 = -16.
Question 7.
Solve for x : 2(7 + x) – 10 = 16 – 2 (x – 24).
Answer:
14 + 2x – 10 = 16 – 2x + 48
2x + 2x = 16 + 48 – 14 + 10
4x = 60 ⇒ x = 15
Question 8.
Convert the ratio 3: 5 into percentages.
Answer:
3: 5= \(\frac{3}{5}\) × 100% = 3 × 20% = 60%.
Question 9.
Define perpetuity.
Answer:
If annuity payments are made for an infinite period then it is called a perpetuity.
Question 10.
Convert 450° into radians.
Answer:
450° = 450 × \(\frac{\pi}{180}=\frac{45 \pi}{18}=\frac{5 \pi}{2}\)
![]()
Question 11.
The average age of 10 boys in a class is 13 years. What is the sum of their ages?
Answer:
Sum of their ages =10 × 13 = 130
Question 12.
Find the slope of the line 2x + 5y – 11 = 0
Answer:
Slope of the line 2x + 5y – 11 = 0 is \(\frac{-a}{b}=\frac{-2}{5}\)
PART-B
II. Answer any Ten questions. (10 × 2 = 20)
Question 13.
Find the number which when divided by 36,40 and 48 leaves the same remainder 5,
Answer:
Let us find out the LCM of 36, 40, 48
36 = 22 × 32
40 = 23 × 5
48 = 24 × 3
LCM = 24 × 32 × 51
= 16 × 45
= 720
Since 5 has to be the remainder, we have to add 5 to 720 i.e. 720 + 5 = 725
Question 14.
If A = {1,23, 4) and B = (34, 5, 6) and U = {1,2, 3,4, 5,6, 7,8)
Verify (A ∪ B)’ =A’ ∩ B’
Answer:
A ∪ B = {1,2,3,4,5,6}
(A∪B)’ = (7,8)
A’ = {5, 6,7,8) B’ = {1,2, 7,8)
A’∩ B’ = {7, 8)
∴ (A∪B)’ = A’ ∩ B’
Question 15.
Find the number of positive divisors and the sum of all positive divisors of 1200.
Answer:
1200 = 24 × 52 × 31 = P1α1 × P2α2 × P3α3
P1 = 2; P2 = 5; P3 = 3
α1 = 4; α2 = 4; α3 = 1
T(n) = (1 + α1)(1 + α2)(1 + α3) = (1 + 4)(1 + 2)(1 + 1) = (5) (3) (2) = 30
Sn = \(\left(\frac{\mathrm{P}_{1}^{\alpha_{1}+1}-1}{\mathrm{P}_{1}-1}\right)\left(\frac{\mathrm{P}_{2}^{\alpha_{2}+1}-1}{\mathrm{P}_{2}-1}\right)\left(-\frac{\mathrm{P}_{3}^{\alpha_{3}+1}-1}{\mathrm{P}_{3}-1}\right)\)
= \(\left(\frac{2^{5}-1^{t}}{2-1}\right)\left(\frac{5^{3}-1}{5-1}\right)\left(\frac{3^{2}-1}{3-1}\right)=\left(\frac{31}{1}\right)\left(\frac{124}{4}\right)\left(\frac{8}{2}\right)\) = 31 × 124 = 3844

Question 16.
Simplify \(\frac{2^{n+1}+2^{n-1}}{2^{n}+2^{n+2}}\)
Answer:

![]()
Question 17.
If a, b, c are in G.P and ax = by = cz show that x, y and z are in H.P
Answer:
a,b,c are in GP
∴ b2 = ac
ax = by = cz = k
ax = k ⇒ a = k1/x
by = k ⇒ b = k1/y
cz = k ⇒ c = k1/z
b2 = ac
(k1/y) = k1/x+1/z
\(\frac{2}{y}=\frac{1}{x}+\frac{1}{z}\)
\(\frac{2}{y}=\frac{x+z}{x z}\)
y = \(\frac{2 x z}{x+z}\)
∴ x, y, z are in HP.
Question 18.
The sum of two numbers is 107 and their difference is 17. Find the numbers.
Answer:

a = 62
a + b =107
b = 107 – a = 107 – 62 = 45
∴ b = 45
Question 19.
Determine the principal which will amounts to ₹ 15000 in 8 years at 41% per annum simple interest
Answer:
H = ₹ 15,000, R = 11, T = 8
A = P + I = P + \(\frac{P+R}{100}\)
1500 = p(1 + \(\frac{\mathrm{TR}}{100}\)) = p(\(\frac{100+8 \times 11}{100}\)) = p\(\left(\frac{188}{100}\right)\) ⇒ p = \(\left(\frac{188}{100}\right)\)
∴ P = ₹ 7978.72
Question 20.
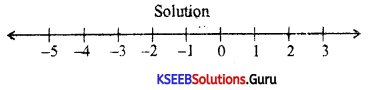
Solve 3x – 2 < 2x + 1 when x is an integer and x is a real number. Also represent on a number line.
Answer:
3x – 2 < 2x + 1
3x – 2x < 2 + 1
x < 3
(i) when x is an integer x = {………- 2, -1, 0, 1, 2}
(ii) when x is a real number x ∈ (-∞, 3)
Question 21.
The average score of 20 boys is 60% and the average score of 30 girls is 70%. Find the combined average.
Answer:
X1 = 60%, N1 = 20
X2 = 70%, N2 = 30
X̄ = \(\frac{X_{1} N_{1}+X_{2} N_{2}}{N_{1}+N_{2}}=\frac{(60)(20)+(70)(30)}{20+30}=\frac{3300}{50}\) = 66%
![]()
Question 22.
If the cost price of 10 articles is equal to the selling price of 9 articles, find the gain percent
Answer:
Let the cost of each article be x.
C.P of 10 articles = 10x
S.P of each article = \(\frac{10 x}{9}\)
S.P of articles = \(\frac{10 x}{9}\) × 10 = \(\frac{100 x}{9}\)
Profit = SP – CP = \(\frac{100 x}{9}\) – 10x = \(\frac{100 x-90 x}{9}=\frac{10 x}{9}\)
Proof% = \(\frac{\text { Profit }}{\text { C.P. }}\) × 100 = \(\frac{\frac{10 x}{9}}{10 x}\) × 100 = \(\frac{10 x}{90 x}\) × 100 = 11\(\frac{1}{9}\)%
Question 23.
Find the value of sin2 \(\frac{\pi}{6}\)cos2 \(\frac{\pi}{3}\) – tan2 \(\frac{\pi}{4}\) + cot2 \(\frac{\pi}{3}\)
Answer:
sin2 \(\frac{\pi}{6}\)cos2 \(\frac{\pi}{3}\) – tan2 \(\frac{\pi}{4}\) + cot2 \(\frac{\pi}{3}\) = \(\left(\frac{1}{2}\right)^{2} \cdot\left(\frac{1}{2}\right)^{2}-(1)^{2}+\left(\frac{1}{\sqrt{3}}\right)^{2}\)
\(\frac{1}{4} \cdot \frac{1}{4}-1+\frac{1}{3}\)
\(\frac{1}{16}-1+\frac{1}{3}=\frac{3-48+16}{48}=\frac{-29}{48}\)
Question 24.
Prove that (SinA + Cos A)2 + (Sin A – CosA)2 = 2
Answer:
LHS (sin A + cos A)2 + (SinA-cos A)2
![]()
Question 25.
Find the equation of the straight line passing through (2, 3) and (3, 4)
Answer:
(x1, y1) = (2, 3) (x2, y2) =(3,4)
\(\frac{y-y_{1}}{x-x_{1}}=\frac{y_{2}-y_{1}}{x_{2}-x_{1}} \Rightarrow \frac{y-3}{x-2}=\frac{4-3}{3-2}\)
⇒ \(\frac{y-3}{x-2}=\frac{1}{1}\) ⇒ y – 3 = x – 2
x – y + 1 = 0
PART-C
III. Answer any ten questions. (10 × 3 = 30)
Question 26.
In a group of 600 people, 150 students were found to be taking tea, 225 like Coffee, 100 like both tea and coffee. Find out how many were taking neither tea nor coffee?
Answer:
n(T) = 150
n(C) =225
n(C ∩ T) = 100
n(∪)=600
n(C ∪ T) = n(C) + n(T) – n(C ∩T) = 225 + 150 – 100 = 375 – 100 = 275
∴ Number of students taking neither coffee nor tea = 600 – 275 = 325
![]()
Question 27.
If R-1 = {(2, 4), (1, 2) (3, 1), (3, 2) Find R. Also find its domain and range.
Sol. R = {(4, 2), (2, 1), (1, 3), (2,3)}
DomR= {1,2,4}
RanR = {1, 2; 3}
Question 28.
Prove \(\sqrt{5}\) is an irrational number.
OR
An electronic device makes a beep after every 60 sec. Another device makes a beep after every 62 sec,. They beeped together at 10 am. Find the time when they will next take a beep together at the earliest.
Answer:
If possible let \(\sqrt{5}\) is a rational number.
\(\sqrt{5}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\), p, q ∈ z, q ≠ 0
we shall also assume that p and q do not have any common factor
∴ 5 = \(\frac{\mathrm{p}}{\mathrm{q}}\)
⇒ p2 = 5q2
∴ p2 is a multiple of 5
∴ 5 divides p2
∴ 5 divides p
∴ p = 5k where k ∈ z, k ≠ 0
p2 = 25k2
5q2 = 25k2 ∵ P2=5q2
q2 = 5k2
∴ q2 is a multiple of 5
∴ 5 divides q2
∴ 5 divides q
∴ 5 divides both p and q
This is a contradiction
∴ Our assumption is wrong
∴ \(\sqrt{5}\) is irrational.
OR

LCM = 22 × 31 × 51 × 31 = 1860 sec = 31 min.
They beeped together at 10am.
∴ After 31 minutes i.e., at 10.31 AM they will next make a beep together at the earliest.
Question 29.
Prove that \(\frac{1}{\log _{2} 4}+\frac{1}{\log _{8} 4}+\frac{1}{\log _{16} 4}\) = 4
Answer:
LHS = \(\frac{1}{\log _{2} 4}+\frac{1}{\log _{8} 4}+\frac{1}{\log _{16} 4}\) = log4 2 + log4 8 + log4 16 = log4(2 × 8 × 16) = log4 256 = log4 44 = 4 log4 4 = 4(1) = 4
Question 30.
The sum of three numbers in an A.P is 15 and their product is 105. Find the numbers.
Answer:
Let the numbers be a – d, a, a + d
sum = 15
a-d + a + a + d = 15
3a = 15 ⇒ a = 15
Product = 105
(a-d) a(a + d) = 105
(5 – d). 5. (5 + d) = 105
(5-d)(5+d) = \(\frac{105}{5}\) = 21
52 – d2 = 21
25 – 21 = d2
d2 = 4
d = 2
∴ The number are a – d, a, a + d,
5-2, 5, 5 + 2
3, 5, 7
![]()
Question 31.
Find the difference between the compound interest and the simple interest on ₹ 5000 invested for 4 years at 8% p.a.
Answer:
P = ₹ 5,000, T = 4yrs, R = 8%
SI = \(\frac{\mathrm{PTR}}{100}=\frac{5000 \times 4 \times 8}{100}\) = 50 × 4 × 8 = 1600
A = P(1 + R)n = 5000(1 + 0.08)8 = 5000 (1.08)4 = 5000 × 1.3604 = 6802.44
∴ CI = 6802.44 – 5000
= 1802.44
Difference between Cl and SI
= CI – SI = 1802.44 – 1600 = ₹ 202.44
Question 32.
Solve the linear inequalities graphically:
5x + 4y ≥ 40, x ≥ 2, y ≥ 3, x, y ≥ 0
Answer:
5x + 4y = 40
y = 0, 5x = 40 ⇒ x = 8, A = (8, 0)
x = 0, 4y = 40 ⇒ y = 10, B= (0, 10)
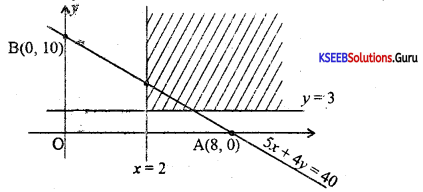
The solution set of each equation is indicated by the arrow mark in the figure. The intersection of these solution sets is in the feasible region shaded as shown in the figure.
Question 33.
Sachin finds by getting out for a duck (0 runs) in the lith innings of his test matches his average of the previous innings is decreased by 5 runs. What is his average after the 11th innings?
Answer:
Let the average after 10 inninngs = x
∴ Total runs after 10 inninngs = 10x
Average after 11 inninngs = x – 5
∴ Total runs after 11 inninngs = 11 (x – 5)
11(x- 5) – 10x = 0
11x- 55 – 10x = 0
x- 55 = 0
x = 55
∴ Average after 11 inninngs = x – 5
= 55 – 5 = 50
![]()
Question 34.
Find the ratio in which the line joining the points (2,5) and (1,9) is divided by the x-axis. Also, find the point of division.
Answer:
P(x, 0) A = (2, 5,) = (x1, y1)
B = (1, 9) = (x2, y2)
P = \(\left[\frac{m x_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\right]=\left[\frac{m(1)+n(2)}{m+n}, \frac{m(9)+n(5)}{m+n}\right]\)
(x, 0) = \(\left[\frac{m+2 n}{m+n}, \frac{9 m+5 n}{m+n}\right]\)
\(\frac{9 m+5 n}{m+n}\) = 0
\(\frac{m}{n}=\frac{-5}{9}\) ⇒ 9m + 5n = 0 ⇒ 9m = – 5n
m :n = 5:9 externally
Taking m = 5, n = 9 to find x use section formula for external division namely,
x = \(\frac{m x_{2}-n x_{1}}{m-n}=\frac{5(1)-9(2)}{5-9}=\frac{5-18}{-4}=\frac{-13}{-4}=\frac{13}{4}\)
P = (\(\frac{13}{4}\), 0) → Point of division.
Question 35.
If an article is sold at ₹ 24 there is a profit of 4 and if it is sold at a loss of 10% find the selling price of the article.
Answer:
SP of the article = ₹ 24
Profit = ₹ 4
CP = SP – Profit = 24 – 4 = ₹ 20
Loss = 10%
We have SP = \(\frac{100-\operatorname{loss} \%}{100}\) × CP = \(\frac{100-10}{100}\) × 20 = \(\frac{90}{100}\) × 20
∴ SP = ₹ 18
Question 36.
If Cot A = \(\frac{5}{12}\) and A is acute, show that 2 cosec A – 4sec A = – \(\frac{247}{50}\)
Answer:
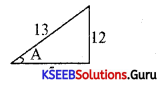
Cosec A = \(\frac{13}{2}\)
Sec A = \(\frac{13}{5}\)
2 cosec A – 4 sec A = 2\(\left(\frac{13}{12}\right)\) – 4\(\left(\frac{13}{5}\right)\) = – \(\frac{494}{60}=-\frac{247}{30}\)
Question 37.
Show that the points A(2, 2) B(6, 3) and C(4, 11) form a right angled triangle.
Answer:
AB = \(\sqrt{(6-2)^{2}+(3-2)^{2}}=\sqrt{16+1}=\sqrt{17}\)
BC = \(\sqrt{(4-6)^{2}+(11-3)^{2}}=\sqrt{4+64}=\sqrt{68}=\sqrt{4 \times 17}\) = 2\(\sqrt{17}\)
CA= \(\sqrt{(4-2)^{2}+(11-2)^{2}}=\sqrt{4+81}=\sqrt{85}\)
AB2 =17, BC2 = 68, CA2 = 85
∴ AB2 + BC2 = CA2
∴ ABC form a right angled triangle.
![]()
Question 38.
If a train travels 15 km / hr faster it would take 1 hour less to travel 180 km, find the original speed of the train.
Answer:
Let s be the actual speed
t be the actual time d = 180 km
s = \(\frac{d}{t}=\frac{180}{t}\) ⇒ t = \(\frac{180}{s}\) ⇒ st = 180
If speed is 15km/hr more then speed becomes s + 15 and time taken will be 1 hour less it becomes t – 1.

∴ Actual speed of the train = 45 km/hr
OR
If α and β are the roots of the equation 2x2 + 5x + 5 = O then find the value of \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}\)
Answer:
α + β = \(\frac{-5}{2}\) and αβ = \(\frac{5}{2}\)
∴ \(\frac{1}{\alpha^{2}}+\frac{1}{\beta^{2}}=\frac{\alpha^{2}+\beta^{2}}{\alpha^{2} \beta^{2}}=\frac{(\alpha+\beta)^{2}-2 \alpha \beta}{(\alpha \beta)^{2}}=\frac{\left(\frac{-5}{2}\right)^{2}-2\left(\frac{5}{2}\right)}{\left(\frac{5}{2}\right)^{2}}=\frac{\frac{25}{4}-5}{\frac{25}{4}}\)
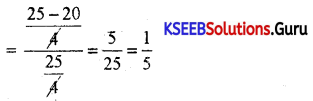
PART – D
IV. Answer any six questions. (6 × 5 = 30)
Question 39.
Let f = {(1, 1), (2, 3), (0, -1)} be a function from Z to Z defined by f(x) = ax + b some integers a and b. (i) Determine a & b. (ii) If f(x) = 2x + 1 g(x) = x2 + 2x + 1 Find (a) fog(2)(b) gof (3)
Answer:
f(x) = ax + b
when x – 1 f(x) = 1
∴ a + b = 1
x = 0 f(x) = -1
a(0) + b = -1 ⇒ b = -1
a + b = 1
a – 1 = 1 ⇒ a = 1 + 1 = 2
∴ a = 2
∴ a = 2, b = -1
(a) fog (2) = f [g(2)] = f [22 + 2(2) + 1]
= f [4 + 4 + 1] = f [9] = 2(9) + 1 = 18 + 1 = 19
(b) gof (3) = g [f(3)] = g [2(3) + 1] – g(7)
= 72 + 2(7) + 1 = 49 + 14 + 1 = 64
Question 40.
Find the sum of all integers between 60 and 400, which are divisible by 13.
Answer:
Sn = 65 + 78 + 91 +……….+ 390
a = 5 d= 13 n = ? Tn = 390
Tn = a + (n – l)d
390 = 65 + (n- 1)13
390 = 65+ 13n-13
13n= 338
∴ n = 26
Sn = \(\frac{\mathrm{n}}{2}\)[a + l] = \(\frac{26}{2}\)(65 + 390)= 13 (455) = 5,915
∴ S = 5,9.15
![]()
Question 41.
The age of the father is 5 times that of the son’s 3 years if the age of the father was 8 times that of his son. Find their present ages.
Answer:
Let the present age of the son = x
Present age of the father = 5x
Three years-agey sons age = x – 3 and fathers age = -5x – 3
Given 5x – 3 = 8(x – 3)
5x – 3 = 8x – 24
8x – 5x = 24 – 3
3x = 21
x = 7
Sons age = x = 7 years
Fathers age 5x = 5(7) = 35 years
Question 42.
A machine depreciates at 10% of its value at the beginning of a year. The cost and scrap value realized at the time of sale are 23240 and 9000 respectively. For how many years the machine was put to use?
Answer:
r= 10% = 0.10 C =23,240 B=9,000 n=?
B = C(1 – r)n
9000 = 23240(1 – 0. 10)
9000 = 23240 (0.90)n
(0.9)n = \(\frac{9000}{23240}\) =0.3872
log (0.9) = log 0.3 872
n log 0.9 = log 0.3872
n = \(\frac{\log 0.3872}{\log 0.9}=\frac{1.5879}{1.9542}=\frac{-1+0.5879}{-1+09542}=\frac{-0.4121}{-0.0458}\)
= 8.99 ≈ 9 years
Question 43.
Calculate the future value of the annuity immediate of ₹ 1000 p.a for 12 years at 16% p.a compounded quarterly?
Answer:
A = ₹ 1,000 p.a, n = 12, R = 16%= 0.6, r = ?, q = 4
r = \(\left(1+\frac{\mathrm{R}}{q}\right)^{q}\) – 1 = \(\left(1+\frac{0.16}{4}\right)^{4}\) – 1 = 0.1698 = 16.98%
F = \(\frac{\mathrm{A}\left[(1+r)^{n}-1\right]}{r}=\frac{1000\left[(1+0.1698)^{12}-1\right]}{0.1698}\)
F = 32,783.17
![]()
Question 44.
Find the equation of the straight line passing through (-2,6) and the sum of the intercepts on the co-ordinate axes is 5.
Answer:
a + b = 5 ⇒ b = 5 – a, Let the equation of the straight line be
\(\frac{x}{a}+\frac{y}{b}\) = 1
\(\frac{x}{a}+\frac{y}{5-a}\) = 1
It passes through (-2. 6) put x = -2, y = 6
\(\frac{-2}{a}+\frac{6}{5-a}\) = 1 ⇒ \(\frac{-10+2 a+6 a}{a(5-a)}\) = 1
⇒ – 10 + 8a = a(5 – a) ⇒ – 10 + 8a = 5a – a2
⇒ a2(a + 5) – 2(a + 5) = 0 ⇒ (a + 5)(a + 2) = 0
⇒ a = 2 ∴ b = 5 – a = 5 – 2 = 3
Case (i)
\(\frac{x}{2}+\frac{y}{3}\) = 1
3x + 2y = 6
3x + 2y – 6 = 0
a = -5
∴ b = 5 – a = 5 – (-5) = 10
Case (ii)
\(\frac{x}{-5}+\frac{y}{10}\) = 1
\(\frac{-2 x+y}{10}\) = 1
-2x + y – 10 = 0
\(\frac{-x}{5}+\frac{y}{10}\) = 1
-2x + y = 10
2x – y + 10 = 0
Question 45.
(a) Form a quadratic equation whose roots are 2 + \(\sqrt{3}\) & 2 – \(\sqrt{3}\)
(b) Evaluate using log. tables \(\frac{(0.5634)^{2} \times(0.0635)}{(2.563)^{2}}\)
Answer:
(a) α = 2 + \(\sqrt{3}\)
β = 2 – \(\sqrt{3}\)
α + β = (2 + \(\sqrt{3}\)) + (2 – \(\sqrt{3}\)) =4
αβ = (2 + \(\sqrt{3}\))(2 – \(\sqrt{3}\)) = 4 – 3 = 1
∴ Quadratic equation’s
x2 – (α + β)x + αβ = 0 ⇒ x2 – 4x+l=0
(b) x = \(\frac{(0.5634)^{2} \times(0.0635)}{(2.563)^{2}}\)
log x = 2log 0.5634 + log 0.0635 – 2log 2.563
= 2 (1.7508) + (2.8027)- 2(0.4087) = 2(-1 + 0.7508) + (-2+ 0.8027) – 2(0.4087)
= -2 + 1.5016-2 + 0.8027-0.8174
= 2.5131 =-2-0.5131
= -2 – 1 + 1-0.5131
= -3 + 0.4869
log x = 3.4869
x = AL[34869] =0.00306
Question 46.
Find the reflection of the point P(2, 1) in the line x + y = 5

Slope of x + y – 5 = 0 is
PQ – x + y – 5 =0
∴ Slope of PQ = +1 =m
∴ Equation of PQ y – y1 =m(x – x1)
y – 1 = 1(x – 2)
y – 1 = x – 2
x – y – 1 = 0
x + y – 5 =0
Add ⇒ 2x – 6 = 0
⇒ x = 3
x – y – 1 = 0
x + y – 5 =0
3 + y – 5 = 0
A = (3, 2) A is the mid point of PQ
∴ A = \(\left(\frac{2+a}{2}, \frac{1+b}{2}\right)\)
(3, 2) = \(\left(\frac{2+a}{2}, \frac{1+b}{2}\right)\)
⇒ \(\frac{2+a}{2}\) = 3
⇒ 2 + a = 6 ⇒ a = 6 – 2
a = 4
⇒ \(\frac{1+b}{2}\) = 3
⇒ 1 + b = 4 ⇒ b = 4 – 1
b = 3
∴ Q = (4, 3)
Question 47.
If x = r cos A cos B, y = r cos A sin B and z = r sin A Then P.T. x2 + y2 + z2 = r2
Answer:
LHS = x2 + y2 + z2 = r2 cos2 A cos2 B + r2 cos2 A sin2 B + r2 sin2 A = r2 cos2 A (cos2 B + sin2 B) + r2 sin2 A= r2 cos2 A(1) + r2 sin2 A = r2 (cos2 A+ sin2 A) = r2 (1) = r2 = RHS
![]()
Question 48.
Find the locus of a point equidistant from (2, 0) and (-2, 0)
Answer:
A = (2, 0), B = (-2, 0)
Let P(x, y) be any point on the locus
∴ PA = PB
PA2 = PB2
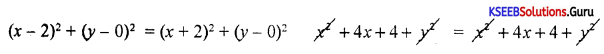
– 4x – 4x + 4 – 4 = 0
– 8x = 0
x = 0
PART-E
IV. Answer any one question. (1 × 10 = 10)
Question 49.
(a) Find the equation of the straight line passing through the intersection of the line 2x + 3y = 5, 7x – y = 6 is perpendicular to the line 3x + 4y + 1 = 0.
(b) If tan A + sin A = m and tanA – sin A = n show that m2 – n2 = ±4\(\sqrt{\mathrm{mn}}\) .
(c) Find the number of digits in 320?
Answer:
(a) 2x + 3y = 5 × 1
7x – y = 6 × 3
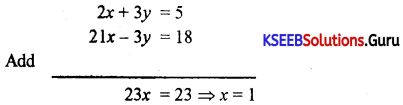
23x = 23 ⇒ x = 1
7x – y = 6
7(1) – y = 6
7 – 6 = y
y = 6
∴ (x1, y1) = (1, 1)
Slope of the given line = \(\frac{-a}{b}=\frac{-3}{4}\)
Required line is perpendicular to given line
∴ slope of the required line = \(\frac{+4}{3}\) = m
∴ Equation of the required line
y – y1 = m(x – x1)
y – 1 = \(\frac{4}{3}\)(x – 1)
3y – 3 = 4x – 4
4x – 3y – 1 = 0
(b) m2 – n2 – (m – n) (m + n)
= (tanA+ sin A- tan A + sin A) (tanA + sin A + tanA- sinA)
= 2 sin A. 2 tan A = 4 sin A tan A = 4 sin A. tan A
(m2 – n2)2 = 16 sin2 A. tan2 A …………..(1)
mn = (tan A + sin A)(tan A – sin A) = tan2 A – sin2 A
= \(\frac{\sin ^{2} A}{\cos ^{2} A}\) – sin2 A = sin2A(\(\frac{1}{\cos ^{2} A}\) – 1) = sin2A\(\frac{1-\cos ^{2} A}{\cos ^{2} A}=\frac{\sin ^{2} A}{\cos ^{2} A}\)sin2A
mn = tan2 A. sin2 A ……….(2)
substitue the value of mn from (2) in (1) we get
(m2 – n2)2 = 16mn
(c) Let x = 320
log x = log 320 = 20log3 = 20[0.4771]
log x = 9.5424
As the characteristic of log x is 9, the number of digits = 9 + 1 = 10.
![]()
Question 50.
(a) Find the sum to n terms of the series: 5 + 55 + 555 +…. n term.
(b) A confectioner makes and sells biscuits. Does he sell one pack of biscuits at ₹ 80? His cost of manufacturing is ₹ 40 per packet as variable cost and 3000 as a fixed cost. Find the
(i) Revenue function
(ii) Cost function
(iii) Profit function
(iv) If he limits his production to 100 packets can he make a profit?
(v) What will be the number of boxes he must sell to make a profit so that he does not incur a loss?
(e) If the product of two numbers is 216 and their LCM is 36. Find their HCF.
Answer:
(a) Let Sn = 5 + 55 + 555 + …….n terms
Sn = 5(1 + 11 + 111 +…….. )
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = 1 + 11 + 111 + ………
Multiply both the sides by 9,
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = 9 + 99 + 999 + …………
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = (10 – 1) + (102 – 1) + (103 – 1) +
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}\) = (10 + 102 + 103 + ……….. ) – (1 + 1 + 1 + ………..)
\(\frac{9 S_{n}}{5}=\frac{10\left(10^{n}-1\right)}{10-1}\) – n
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{5}=\frac{10\left(10^{\mathrm{n}}-1\right)}{9}\) – n
Sn = \(\frac{5}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-n\right]=\frac{5}{9}\left[\frac{10}{9}\left(10^{n}-1\right)-n\right]\), n ∈ N
(b) (a) Revenue function = R (x) = Selling price X quantity
= 80 x (x = No. of pack of biscuit)
(b) Cost function = C (x) = ax + b
= 40x + 3000
(c) Profit function = P (x)
= R(x) – C(x)
= 8Ox – (40x + 3000)
= 80x – 40x – 3000
= 40x – 3000
(d) If x = 100 packets
∴ P(x) = 40x – 3000
P(100) =40 (100)- 3000
= ₹ 1,000
(e) No. of packets required to ensure no Joss (at BEP)
C (x) =R(x)
40x + 3000 = 80 x
3000 = 80x – 40x
3000 = 40x
x = \(\frac{3000}{40}\)
x =75 packet
(c) ab = 216 LCM = 36 HCF = ?
HCF × LCM = ab = 216
HCF = \(\frac{216}{\mathrm{LCM}}\)
HCF = \(\frac{216}{36}\) = 6