1st PUC Basic Maths Model Question Paper 1 with Answers

Students can Download 1st PUC Basic Maths Model Question Paper 1 with Answers, Karnataka 1st PUC Basic Maths Model Question Papers with Answers helps you to revise the complete syllabus.

Karnataka 1st PUC Basic Maths Model Question Paper 1 with Answers

Time: 3.15 Hours
Max. Marks: 100

Instructions:

1. The questions paper consists of five parts A, B, C, D, and E.
2. Part – A carries 10 marks, Part – B carries 20 marks, Part – C curries 30 marks, Part – D carries 30, and Part – E carries 10 marks.
3. Write the question numbers properly as indicated in the questions paper

PART-A

I. Answer any ten questions (10 × 1 = 10)

Question 1.
Define an imaginary number.
Answer:
A number of the form a + ib where a, b ∈ R, the set of real numbers and i = \(\sqrt{-1}\) is called a complex number or an imaginary number.
Example : 2 + 3i

Question 2.
If A = {1, 2} and B = {a, b} then find B × A.
Answer:
B × A={(a, 1),(a, 2),(b, 1 ),(b, 2)}

Question 3.
If f: R → R is defined by f(x) = 2x + 3 then find f(\(\frac{1}{2}\))
Answer:
f(\(\frac{1}{2}\)) = 2(\(\frac{1}{2}\)) + 3 = 1 + 3 = 4

Question 4.
Simplify \(\left(\frac{81}{256}\right)^{\frac{1}{4}}\)
Answer:
\(\left(\frac{8}{256}\right)^{1 / 4}=\left(\frac{3^{4}}{4^{4}}\right)^{1 / 4}=\left\{\left(\frac{3}{4}\right)^{4}\right\}^{1 / 4}=\frac{3}{4}\)

Question 5.
Find the value of log_0.1 10
Answer:
Let log_0.1 10 = x ⇒(0.1)^x ⇒ \(\left(\frac{1}{10}\right)^{x}\) = 10
⇒ 10^-x = 10¹ ⇒ -x = 1 ⇒ x = -1
∴ log_0.1 = 10 = -1

Question 6.
Find the nature of the roots without solving the equation x² – x + 1 = 0
Answer:
a = 1, b = -1, c = 1
Δ = b² – 4a = (-1)² – 4(1)(1) = 1 – 4 = -3 < 0
Δ < 0
∴ The roots are complex.

Question 7.
What is the present value of an income of 1000 a year to be received forever? Assume the discount rate to be 12%.
12%
Answer:
A = ₹ 1,000, r = 12% = \(\frac{12}{100}\) = 0.12,
P_∞ = A/r = \(\frac{1000}{0.12}\) = ₹ 8333.33

Question 8.
Convert \(\frac{1}{4}\) into percentage
Answer:
\(\frac{1}{4}=\frac{1}{4}\) × 100% = 25%

Question 9.
Define a radian
Answer:
A radian is an angle subtended at the center of a circle by an arc of the circle such that the length of the arc is equal to the radius of the die circle.

Question 10.
Convert 315° into radians
Answer:
315° = 315 × \(\frac{\pi}{180}=\frac{7 \pi^{c}}{4}\)

Question 11.
If the slope of the line AB is \(\) and AB ⊥ CD then find the slope of CD.
Answer:
m₁ = \(\frac{3}{4}\), m₂ = ?
AB ⊥ CD
∴ m₁ × m₂ = -1 ⇒ \(\frac{3}{4}\) × m₂ = 1 ⇒ m₂ = – \(\frac{4}{3}\) = slope of CD

Question 12.
Find the centroid of the triangle formed by the points (2, 4), (5, 3), and (8, 3)
Answer:
G = \(\left(\frac{2+5+8}{3}, \frac{4+3+3}{3}\right)=\left(\frac{15}{3}, \frac{10}{3}\right)=\left(5, \frac{10}{3}\right)\)

PART-B

II. Answer any Ten questions. (10 × 2 = 20)

Question 13.
Find the number of positive divisors of 960
Answer:
960
960 = 26 × 31 × 51
p₁ = 2, α₁ = 6, p₂ = 3, α₂ = 1, p₃ = 5, α₃ = 1
T(n) = (1 + α₁)(1 + α₂)(1 + α₃)
T(960) = (1 + 6)(1 + 1)(1 + 1) = (7)(2)(2) = 28

Question 14.
If A =(1, 3,5, 7,9) and B = (2,4,6,8, 10, 12) define a function f: A → B by f(x) = x + 1 ∀ x ∈ A, verfiy that the function is one – one and onto
Answer:
f: A → B is one-one but not onto as 12 has no pre-image.

Question 15.
Simplify \(\left(\frac{x^{2}}{x^{b}}\right)^{n+b}\left(\frac{x^{b}}{x^{c}}\right)^{b+c}\left(\frac{x^{c}}{x^{2}}\right)^{c+x}\)
Answer:
(x^a-b)^a+b(x^b-c)^b+c(x^c-a)^c+a = x^a2-b2.x^b2-c2.x^c2-a2
= \(x^{a^{2}-b^{2}+b^{2}-c^{2}+c^{2}-a^{2}}\) = x° = 1

Question 16.
Prove that log₂ [log₂ [log₂ 16]] = 1
Answer:
Log₂ [log₂[log₂16]] = log₂ [log₂[log₂ 24]] = log₂[log₂[4log₂ 2]] = log₂ [log₂ [4(1)]]
= log₂ [log2 4] = log₂ [log₂ 22] = log₂ [2 log₂ 2] = log₂ [2(1)] = log₂ 2 = 1 [∵ log_a o = 1]

Question 17.
Is -300 a term of the A.P. 10, 7, 4….. ?
Answer:
a =10, d = 7 – 10 = -3
T_n = a + (n- 1) ⇒ -300= 10 + (n – 1) (-3)
⇒ -300 = 10 – 3n + 3 ⇒ 3n = 10 + 3 + 300
∴ 3n = 313
∴ n = \(\frac{313}{3}\) ∉ N
∴ n being number of terms cannot be a fraction.
∴ -300 is not a term of the A.P

Question 18.
If k + 9, k – 6, 4 are in GP then find the value of K.
Answer:
(k – 6)² = (k + 9)4
k² – 12k + 36 = 4k + 36 ⇒ k² – 12k – 4k + 36 – 36 = 0
k² – 16k =0 ⇒ k(k – 16) = 0
k =0, k= 16

Question 19.
If a and p are the roots of the equation x² – x + 2 = 0 then show that α²β + β²α = 2
Answer:
α + β = \(\frac{-b}{a}=\frac{-(-1)}{1}\) = 1 and αβ = \(\frac{c}{a}=\frac{2}{1}\) = 2
α²β + αβ² = αβ(α + β) = 1(2) = 2

Question 20.
Sove 5x – 3 < 3x + 1 when x is an integer and x is a real number
Answer:
5x – 3 < 3x + 1
2x <4

5x – 3x < 3 + 1
⇒ x < 2

1. x = {…………..-2, -1,0, 1} x ∈ Z
2. x ∈ (-h, 2) x ∈ R

Question 21.
Sowmya invested ₹ 1500 for 8 years and Anisha invested ₹ 7500 for 3 years at the same rate of interest. If altogether they received ₹ 1725 as interest find the rate of simple interest charged.
Answer:
Sowmya,
P₁ = 1500, T₁ = 8, R₁ = R
I₁ = \(\frac{1500 \times 8 \times \mathrm{R}}{100}\) = 120R

Anisha,
P₂ = 7500 T₂ = 3 R, = R
I₂ = \(\frac{7500 \times 3 \times R}{100}\) = 225R
I₁ + I₂ = 1725
120 R + 225 R = 1725
345 R = 1725 ⇒ R = \(\frac{1725}{345}\) = 5%

Question 22.
If the cost price of a machine is ₹ 150 and selling price is ₹ 100 find the loss percentage?
Answer:
CP = ₹ 150 . SP = ₹ 100
CP > SP
∴ loss
loss = CP – SP = 150- 100 = ₹ 50
loss% = \(\frac{\text { loss }}{\mathrm{CP}}\) × 100 = \(\frac{50}{150}\) × 100 = 33.3%

Question 23.
The average score of 20 boys is 60% and the average score of 30 girls is 70%. Find the combined average of boys and girls?
Answer:
X₁ = 60%, N₁ = 20; X₂ = 70%, N₂ = 30
X̄₁₂ = \(\frac{\mathrm{X}_{1} \mathrm{~N}_{1}+\mathrm{X}_{2} \mathrm{~N}_{2}}{\mathrm{~N}_{1}+\mathrm{N}_{2}}=\frac{(60)(20)+(70)(30)}{20+30}=\frac{3300}{50}\) = 66%

Question 24.
Derive the equation of the line in one point form. i.e. y – y₁ = m (x – x₁) geometrically, where m is the slope and p(x₁ y₁) is the given point
Answer:

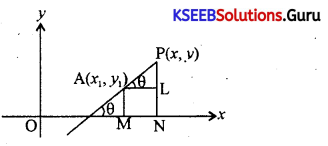
Slope of AP = m = tan θ = \(\frac{\mathrm{PL}}{\mathrm{AL}}=\frac{\mathrm{PN}-\mathrm{NL}}{\mathrm{MN}}=\frac{\mathrm{PN}-\mathrm{AM}}{\mathrm{ON}-\mathrm{OM}}=\frac{y-y_{1}}{x-x_{1}}\)

∴ y – y₁ = m(x – x₁)

Question 25.
Find the value of x if the distance between (x, 3) and (4, 5) is “5 units”.
Answer:
A = (x, 3), B = (4, 5)
AB =5
\(\sqrt{(x-4)^{2}+(3-5)^{2}}\) =5
(x- 4)² + 4= 25
x² – 8x + 16 + 4 – 25 =0
x² – 8x – 5 = 0
x = \(\frac{-(-8) \pm \sqrt{64-4(1)(-5)}}{2(1)}=\frac{8 \pm \sqrt{64+20}}{2}=\frac{8 \pm \sqrt{84}}{2}=\frac{8 \pm 2 \sqrt{21}}{2}=\frac{2(4 \pm \sqrt{21})}{2}\)
x = 4 ± \(\sqrt{21}\)

PART-C

III. Answer any ten questions. (10 × 3 = 30)

Question 26.
Prove the \(\sqrt{2}\) is an irrational number. Sol. We shall prove it by contradiction.
Answer:
We shall prove it by contradiction
If possible, Let \(\sqrt{2}\) be a rational number
Let \(\sqrt{2}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) where p and q are integers and q ≠ 0.
Further let p and q are coprime i.e. H.C.F. of p and q = 1.
\(\sqrt{2}\) = \(\frac{\mathrm{p}}{\mathrm{q}}\) ⇒ \(\sqrt{2}\)q = p ,
⇒ 2q² = p²
⇒ 2 divides p² ⇒ 2 divides p ⇒ p is even
Let p = 2k where k is an integer p² = 4k²
2q² = 4k²
q² = 2k² q² is even
⇒ q is even
Now p is even and q is even which implies p and q have a common factor 2. which is a contradiction of the fact that p and q are co-prime.
∴ our assumption that \(\sqrt{2}\) is rational is wrong and hence \(\sqrt{2}\) is irrational.

Question 27.
Define an equivalence relation with an example. Also, give an example of a relationship that is only symmetric.
Answer:
A relation R on a non-empty set A is called an equivalence relation if it is reflexive, symmetric, and transitive.
Example: On a set of straight lines in a plane the relation “parallel to” is an equivalence relation. Let A= {1, 2, 3} R = {(1, 1), (3, 3), (2, 1), (1, 2)}
R is symmetric but not reflexive and not transitive.

Question 28.
If a^x = b^y = c^z and b² = ac. Show that \(\frac{1}{x}+\frac{1}{x}=\frac{2}{y}\)
Answer:
Let a^x = b^y = c^z = k (say)
∴ a^x = k ⇒ a = k 1/x,
b^y = k ⇒ b = k 1/y,
c^z = k ⇒ c = k’*
Now, b² = ac
∴ (k ^1/y)² = ,k^1/x. k^1/z
∴ k^2/y = k^{1/x + 1/z}.
Bases are same
∴ Equating powers on both the sides, we get.
\(\frac{2}{y}=\frac{1}{x}+\frac{1}{z}\)

Question 29.
Find the number of zeroes in (0.2)100 after the decimal point and the first significant figure.
Answer:
log (0.2)¹⁰⁰ = 100 log 0.2= 100 (T. 0.3010)= 100(-1 + 0.3010) = – 100 + 30.10
= -100 + 30 + 0.10 = -70 + 0.10 = 70.10
characteristic = 70
∴ number of zeroes = 70 – 1 = 69.

Question 30.
Find the sum of the following series : 7 + 77 + 777 + 7777 +……… n terms.
Answer:
Let S_n = 7 + 77 + 777…………..n terms
= 7 [1 + 11+ 111 +………..to n terms]
= \(\frac{7}{9}\) [9 + 99 + 999 + …………..to n terms]
= \(\frac{7}{9}\) [(10- 1) + (100 – 1) + (1000 – 1)…………..to n terms]
= \(\frac{7}{9}\left[\frac{10\left(10^{n}-1\right)}{10-1}-n\right]\) [∵ 10 + 10² + 10³ ……… to n terms is in G.P
where a = 10, r = 10]

S_n = \(\frac{7}{9}\left[\frac{10\left(10^{n}-1\right)}{9}-\mathrm{n}\right]\)

Question 31.
A father is 28 years older than a son. After 5 years the father’s age will be 7 years more than twice that of the son. Find their present ages.
Answer:
Let father’s age be x years and son’s age be y years.
Given: x – y = 28……………….(1)
After five years father’s age is x + 5 and son’s age is y + 5.
Also given: x + 5 = 2(y + 5) + 7
x + 5 = 2y + 10 + 7
Solving (1) and (2), we get: x = 44 and y = 16
Thus father’s age is 44 years and the son’s age is 16.

Question 32.
Solve the linear inequalities graphically: x +3y ≥ 3, 2x + y ≥ 2, x ≥ 10, y ≥ 0
Answer:

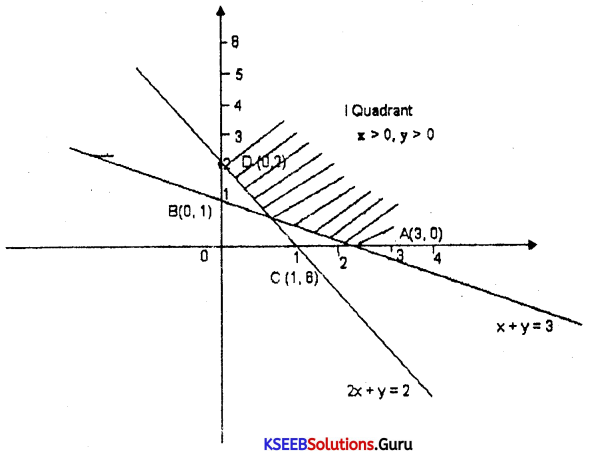
Question 33.
In what time a sum of ₹ 500 will earn ₹ 975 at the rate pf 6% p.a if the compound interest is payable half yearly?
Answer:
R = 6% = \(\frac{6}{100}\) = 0.06
q = 4
r = \(\left(1+\frac{R}{q}\right)^{q}\) – 1 = 0.0607
A = P(1 + r)ⁿ
log A= log P + n log (1 + r)
n = \(\frac{\log A-\log P}{\log (1+r)}=\frac{\log 975-\log 500}{\log (1+0.0607)}=\frac{2.9890-2.6990}{0.0256}\) = 11.33 years

Question 34.
Insert 4 arithmetic means between 5 and 10.
Answer:
Let A₁, A₂, A₃, A₄ be the 4 A.M’s between 5 and 10
∴ 5, A₁, A₂, A₃, A₄, 10 are in A.P,
Last element is 6th element a + 5d = 10
5 + 5d =10
5d = 10-5
5d = 5
∴ A. M’s are 6,7, 8, 9

Question 35.
By how many percent should the use of tea be increased if the price of tea is decreased by 10% so that the expenditure remains unchanged.
Answer:
Let Price be 100 Let Quantity be 100
Total expenditure = 100 × 100 = 10,000
Then New Price = 100 – 10 = 90
Let New Qty = y
Total expenditure = 90 y
90 y = 10,000
Increase = 111.11 – 100 = 11.11
∴ % increase = \(\frac{\text { increase }}{\text { Original value }}\) × 100 = \(\frac{11.11}{100}\) × 100 = 11.11%

Question 36.
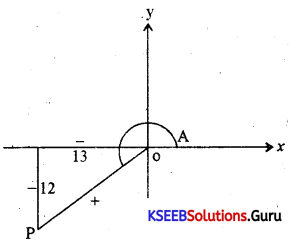
If tan A = \(\frac{12}{13}\) and 180 < A < 270. Find the value of \(\frac{3 \sin A-2 \cos A}{9 \cos A+4 \sin A}\)
Answer:
OP² = OM² + MP² = 169 + 144 = 313
OP = \(\sqrt{313}\)
SinA = \(\frac{-12}{\sqrt{313}}\)
CosA = \(\frac{-13}{\sqrt{313}}\)

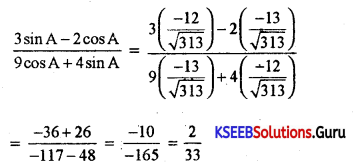
Question 37.
Show that the straight lines 2x – 3y = 7,3x – 4y =13, 8x – 11y = 33 are concurrent. Also find the point of concurrency. .
Answer:
2x – 3y = 7 × 3
3x – 4y = 7 × 2

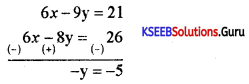
y = 5
2x-3y = 7 ⇒ 2x – 3(5) = 7 ⇒ 2x – 15 = 7 ⇒ 2x = 22 ⇒ x = 11
Put x =11 y = 5 in 8x- 11y = 33
8 (11) – 11 (5) = 88 – 55 =33 .
∴ The three lines are concurrent. Point of concurrency = (11, 5)

Question 38.
Find the distance between two parallel lines 3x + 4y + 5 = 0 and 6x + 8y + 20 = 0
Answer:
3x + 4y + 5 = 0 × 2
6x + 8y + 10 = 0 ……(1)
6x + 8y + 20 = 0 ………(2)

PART – D

IV. Answer any six questions. (6 × 5 = 30)

Question 39.
In a group of 150 people, 70 like Cricket, 30 like hockey and cricket both. How many like Cricket only and not hockey? How many like hockey? Show the result using the Venn diagram.
Answer:
n(C∪A)=150 n(C) = 70 n(H) = ? n(C∩H) = 30
n(C∪H) = n(C) + n(H) – n(C∩H)
150 = 70 + n(H) – 30
150 = 40 + n(H) [∵ n(H) = 110]
n(C – H) = n(C) – n(C∩H) = 70 – 30 = 40 .

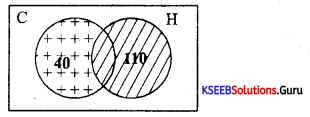
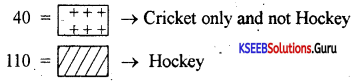
Question 40.
Evaluate using log, tables \(\frac{42.15 \times(0.2713)^{2}}{0.8932}\)
Answer:
Let x = \(\frac{42.15(0.2713)^{2}}{0.8932}\)
log x = log 42.15+ 21og 0.2713-log 0.8932
= 1.6247+ 2(1.433)-(). 9509)= 1.6247+ 2(-l + 0.433)-(1.9509)
= 1.6247-2 +0.866-(-1 + 0.9509)= 1.6247-2+ 0.866-(-1 + 0.9509)
= 1.6247-2 + 0:866+ 1 -0,9509
log x = 0.5398 =AL [0.5398] = 3.4733
∴ x = 3.4733

Question 41.
Find the sum of the series : 4 + 44 + 444 + ….. n terms,
Answer:
Let S_n = 4 + 44 + 444 + n terms
S_n = 4 (1 + 11 + 111 + ……….)
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{4}\) = 1 + 11 + 111 + ……
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{4}\) = 9 + 99 + 999
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{4}\) = (10 – 1) + (102 – 1) + (103 – 1) + ………
\(\frac{9 \mathrm{~S}_{\mathrm{n}}}{4}\) = (10 + 102 + 103 + ………) – (1 + 1 + 1 + …………….)
\(\frac{9 S_{n}}{4}=\frac{10\left(10^{n}-1\right)}{10-1}\) – n
\(\frac{9 S_{n}}{4}=\frac{10\left(10^{n}-1\right)}{9}\) – n
S_n = \(\frac{4}{9}\left[\frac{10}{9}\left(10^{n}-1\right)-n\right]\), n∈N

Question 42.
The cost of 2 kgs of sugar and 5 bags of dhal is ₹ 90. The cost of 5 kgs of sugar and 2 kgs of dhal is ₹ 120. Find the cost of sugar and dhal per kg.
Answer:
Let the cost of 1kg of sugar = x and cost of 1 kg of dhal = y
2x + 5y = 90 × 2
5x + 2y – 120 × 5

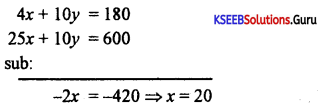
2x + 5 = 90
2(20) + 5y = 90
5y = 90 – 40 = 50
y = 10

∴ cost of 1 kg of sugar = ₹ 20
cost of 1 kg of dhal = ₹ 10

Question 43.
Govindappa bought 51 bags in the wholesale market at an average price of ₹ 318 each. The price of 33 leather bags was ₹ 426 each. The price of the remaining cotton bags forms an increasing Arithmetic progression. If the price of the costliest cotton bag was ₹ 150/ – find the price of the cheapest cotton bag.
Answer:
Average price of 11 bags = Rs.450
Total price of 11 bages = 11 × 450 = 4950
Average price of 7 leather bags = Rs. 575
Total price of 7 leather bags = 575 × 7 = 4025
The price of the remaining 4 cotton bags from an increasing A.P, Whose first term be a and common difference d,
1 = 300, n = 4, Sn = 925.
Sum of remaining 4 bags = 4950 – 4025 = 925
Sn =925
\(\frac{\mathrm{n}}{2}\) (a + 1) = 925
\(\frac{4}{2}\) (a + 300) = 925
2 (a + 300) = 925
2a + 600 = 925
2a = 325
a = \(\frac{325}{2}\) =162.50
Price of the cheapest cotton bag = Rs. 162.50

Question 44.
The daily cost of production ‘C is 1₹ and ‘x’ unit of an assembly is C(x) = 3.5x + 1200. If each unit is sold for 6 then find the minimum number of units that should be produced and sold to ensure no loss. If the selling price is increased by half a rupee a unit then what would be the Break-Even Point.
Answer:
C(x) = 3.5x + 1200
R(x) = C(x) for a break even point
R(x) = 6x
6x = 3.5x + 1200
6x – 3.5x = 1200
2.5x = 1200
x = \(\frac{1200}{2.5}\) = 480 units

If the S.P is increased by ₹ 0.5 a unit then
R(x) = 6.5x
R(x) = C(x)
6.5x = 3.5x + 1200
6.5x – 3.5x = 1200
3x = 1200
x = 400 units

Question 45.
Prove that sec²\(\frac{5 \pi}{4}\) cosec²\(\frac{5 \pi}{4}\) – sin²\(\frac{3 \pi}{4}\)cos²\(\frac{4 \pi}{3}\) = 31/8
Answer:
sec\(\frac{5 \pi}{4}\) = sec 225 = sec(180+45°) = Sec45° = – \(\sqrt{2}\)
cosec\(\frac{5 \pi}{4}\) = coscc 225° = cosec (180 + 45) = cosec 45° = – \(\sqrt{2}\)
sin \(\frac{3 \pi}{4}\) = sin 135°= sin(180 – 45°)sin45° = \(\frac{1}{\sqrt{2}}\)
cos \(\frac{4 \pi}{3}\) = cos 240 = cos (180 + 60) = – cos 60 = –\(\frac{1}{2}\)
∴ LHS = sec²\(\frac{5 \pi}{4}\) cosec²\(\frac{5 \pi}{4}\) – sin²\(\frac{3 \pi}{4}\) cos²\(\frac{4 \pi}{3}\)

= \((\sqrt{2})^{2} \cdot(\sqrt{2})^{2}-\left(\frac{1}{\sqrt{2}}\right)^{2} \cdot\left(\frac{-1}{2}\right)^{2}\)
= 2.2 – \(\frac{1}{2}\).\(\frac{1}{4}\) = 4 – \(\frac{1}{8}\) = \(\frac{32-1}{8}=\frac{31}{8}\) = R.H.S

Question 46.
Derive the section formula for the internal division if A (x₁, y₁) and B (x₂, y₂) are the two given points and P(x, y) be the point that divides the join of AB in the ratio m:n Sol. Let X’ OX and YOY’ be the axes.
Answer:
Let P (x₁, y₁), Q (x₂, y₂) be the given points?
Let R (x, y) be the point that divides PQ internally in the ratio m:n.

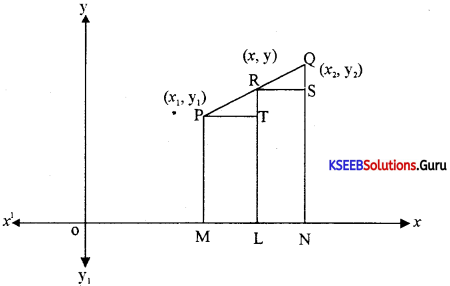
The Δles PRT and RQS are similar
∴ \(\frac{\mathrm{PT}}{\mathrm{RS}}=\frac{\mathrm{RT}}{\mathrm{QS}}=\frac{\mathrm{PR}}{\mathrm{RQ}}\)
\(\frac{\mathrm{PT}}{\mathrm{RS}}=\frac{\mathrm{PR}}{\mathrm{RQ}}\)
⇒ \(\frac{\mathrm{PT}}{\mathrm{RS}}=\frac{\mathrm{m}}{\mathrm{n}}\) (from (1))
⇒ \(\frac{\mathrm{ML}}{\mathrm{LN}}=\frac{\mathrm{m}}{\mathrm{n}}\)
⇒ \(\frac{\mathrm{OL}-\mathrm{OM}}{\mathrm{ON}-\mathrm{OL}}=\frac{\mathrm{m}}{\mathrm{n}}\)
\(\frac{x-x_{1}}{x_{2}-x}=\frac{m}{n}\)

n (x – x₁) = m (x₂ – x)
⇒ nx – nx₁ = mx₂ – mx
⇒ mx – nx = mx₂ – nx₁
⇒ (m + n) x = mx₂ – nx₁
⇒ x = \(\frac{m x_{2}+n x_{1}}{m+n}\)
\(\frac{\mathrm{RT}}{\mathrm{QS}}=\frac{\mathrm{PR}}{\mathrm{RQ}}\)
⇒ \(\frac{\mathrm{RT}}{\mathrm{QS}}=\frac{\mathrm{m}}{\mathrm{n}}\)
⇒ \(\frac{\mathrm{RL}-\mathrm{TL}}{\mathrm{QN}-\mathrm{SN}}=\frac{\mathrm{m}}{\mathrm{n}}\)
⇒ \(\frac{\mathrm{RL}-\mathrm{PM}}{\mathrm{QN}-\mathrm{RL}}=\frac{\mathrm{m}}{\mathrm{n}}\)
⇒ \(\frac{y-y_{1}}{y_{2}-y}=\frac{m}{n}\)
⇒ ny- ny₁ = my₂ – my
⇒ my – ny = my₂ – ny₁
⇒ (m – n)y = my₂ – ny₁
⇒ y = \(\frac{\mathrm{my}_{2}+\mathrm{ny}_{1}}{\mathrm{~m}+\mathrm{n}}\)
The coordinates of R are
(x, y) = \(\left(\frac{m y_{2}+n x_{1}}{m+n}, \frac{m y_{2}+n y_{1}}{m+n}\right)\)
This is called the section formula for the internal point of division.

Question 47.
Find the equation of the locus of the point which moves such that the ratio of its distances (2, -3) and (4, -2) is 2 : 3.
Answer:
A = (2,-3), B = (4,-2)
Let P(x, y) be any point on the locus
\(\frac{\mathrm{PA}}{\mathrm{PB}}=\frac{2}{3}\) ⇒ 3PA = 2PB

3\(\sqrt{(x-2)^{2}+(y+3)^{2}}\) = 2\(\sqrt{(x-4)^{2}+(y+2)^{2}}\)
9[(x – 2)² + (y + 3)²] = 4[(x – 4)² + (y + 2)²]
9[x² – 4x + 4 + y² + 6y + 9] = 4[x² – 8x + 16 + y² + 4y + 4]
9[x² – y² – 4x + 6y + 13] = 4[x² + y² – 8x + 4y + 20]
9x² + 9y² – 36x + 54y + 117 = 4x² + 4y² – 32x + 16y + 80
9x² – 4x² + 9y² – 4y² — 36x + 32x + 54y – 16y + 117 – 80 = 0
5x² + 5y² – 4x + 38y + 37 = 0

Question 48.
Find the equation of the line which passes through the point of intersection of the lines x – 2y + 4 = O and 4x – 3y + 1 = 0 and is inclined at an angle of 135° with the x-axis.
Answer:
x – 2y + 4 = 0 × 1
4x – 3y + 1 = 0 × 1

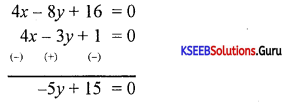
5y = 15
y = 3
x – 2y + 4 = 0
x – 2 = 0

x – 6 + 4=O
x = 2

∴ The point of intersection = (2, 3)
θ = 135°
m = tanθ = tan 135 = tan(180 – 45) = -tan45°= -1

∴ Equation of the required line ¡s
y – y₁ = m(x – x₁) ⇒ y – 3 = -1(x – 2)
y – 3 = -x + 2
x + y – 5 = 0

PART – E

IV. Answer any One Question. (1 × 10 = 10)

Question 49.
(a) Find the domain and Range of the function.
f(x) = \(\frac{x^{2}+2 x+1}{x^{2}-8 x-12}\) where x ∈ R
(b) What is the future value of 1000 deposited annually years for 12 gathering compound interest at 16%?
(c) Form the cubic equation whose roots are 3, 5 and 7
Answer:
(a) f(1) = \(\frac{4}{-19}=\frac{4}{19}\)
f(3) = \(\frac{9+6+1}{9-24+12}\)
= \(\frac{16}{-3}\)
f(5) = \(\frac{5^{2}+10+1}{5^{2}-8(5)+12}\)
= \(\frac{36}{-3}\) = – 12
Domain = { 1, 3, 5 ………….}
Range = {-4/19, -16/3, -12 …………..}

(b) A = 1000, n = 12, r = 0.16
F = \(\frac{\mathrm{A}\left[(1+r)^{n}-\right]}{r}=\frac{100\left[(1+0.16)^{12}-1\right]}{0.16}=\frac{1000\left[(1.16)^{12}-1\right]}{0.16}\) = 30.850.16

(c) (x – 3)(x – 5)(x – 7) =0 ⇒ (x – 3)(x² – 5x – 7x + 35) =0
⇒ (x – 3)(x² – 12x + 35) 0 ⇒ x³ – 12x² + 35x – 3x² + 36x – 105 =0
x³ – 15x² + 71x – 105 = 0

Question 50.
(a) Find the value of x
If \(\frac{x \cdot \sin ^{2} 300 \cdot \sec ^{2} 240}{\cos ^{2} 225 \cdot {cosec}^{2} 240}\) = cot2 315°. tan 300
(b) Find the equation of the line perpendicular to 3x – 2y + 1 = O and passing through the point (1, -2)
(c) Insert two geometric means between 1 and 1//27
Answer:
sin 300 = sin (360 – 60) = – sin 60 = \(\frac{\sqrt{3}}{2}\)
sec 240 = sec(180 + 60)= – sec60°= – 2
cos 225 = cos(180 + 45°) – cos45°= – \(\frac{1}{\sqrt{2}}\)
cosec 240 = cosec (180 + 60°) = – cosec 60 = – \(\frac{2}{\sqrt{3}}\)
cot 315° = cot (360 – 45°) = – cot 45° = – 1
tan 300 = tan (360 – 60°) = – tan 600 = – \(\sqrt{3}\)

∴ The given equation becomes:
\(\frac{x \cdot \frac{3}{4} \cdot 4}{\frac{1}{2}, \frac{4}{3}}\) = 1.3
⇒ x = \(\frac{6}{9}=\frac{2}{3}\)

(b) Slope of the given line 3x – 2y + 1 = 0 is \(\frac{3}{2}\) = m1
Since the two lines are perpendicular m₁ m₂ = – 1
∴ m₂ = \(\frac{-1}{m_{1}}=\frac{-1}{3 / 2}=\frac{-2}{3}\)

Thus the equation of the ime vith slope m = \(\) and passing through
(x₁ y₁) (1, -2) is given by
⇒ y -y₁ = m(x – x₁)
⇒ y – 2 = (x – 1)
⇒ 3y – 6 = – 2x + 2
⇒ 2x + 3y + 4 = 0

(c) 1, g, g₂, \(\frac{1}{27}\)
a = 1, T_n = \(\frac{1}{27}\), r =?, n = 4
T_n = ar^n-1 ⇒ \(\frac{1}{27}\) = 1.r³
⇒ \(\left(\frac{1}{3}\right)^{3}\) = r³
⇒ r = \(\frac{1}{3}\)
∴ 1, 1/3, 1/9, 1/21
∴ Geometric means are 1/3, 1/9